![[레벨:30]](https://gujoron.com/xe/modules/point/icons/default/30.gif "포인트:674221point, 레벨:30/30"){kind=icon}
김동렬|
구조론 수학을 어디에 써먹을 것인가? 삼총사라고 한다. 학창시절에 꼭 붙어다니는 친구는 자신을 포함하여 3명이 적당하다. 4명이면 깨진다. 3이 ‘완전수’다. 1은 친구가 없고, 2는 친구가 있고, 3은 친구가 적당하고, 4는 친구가 깨진다. 여기서 ‘완전수’의 의미는 위상의 균일에 있다. 친구간에 위상의 균일은 정보공유에 의해 결정된다. 정보격차에서 일진과 이진으로 계급이 나눠진다. 정보를 공유하지 않는 친구는 물론 많을수록 좋다. 삼총사는 되는데 사총사는 잘 안 된다. 4명이면 정보공유가 불가능해지고 한 명이 왕따된다. 4명이 토론하여 의사결정을 하려면 사건의 시시콜콜한 내막을 들추어야 하고 그 경우 도리어 오해가 발생하여 의사결정이 어렵게 된다. 토론하지 않고 이심전심으로 의사결정할 수 있는 숫자는 3이다. 구조론의 수는 5다. 그런데 왜 3인가? 3에다 정보의 입출력을 더하면 5가 되기 때문이다. 입력 1> 의사결정 3> 출력 1로 합이 5다. 3이 저울의 축과 날개가 되어 의사결정을 하는 것이다. 3은 다수결이 필요없다. 두 사람이 찬성하면 세 번째 사람은 자동으로 찬성한다. 그러나 일은 4명이 적당하다. 이때 4명이 정보를 공유하고 일거리가 나머지 1을 채워 5를 이룬다. 이때 의사결정은 없다. 정해진 일을 반복하는 것이다. 예컨대 공부모임을 만들려면 4명으로 해야 한다. 만약 5명이 스터디그룹을 만들면 깨질 확률은 급속하게 높아진다. 5명이 스터디 그룹을 한다면 그 중의 한 명은 대장을 맡아야 한다. 그렇게 하지 않으면 점점 놀이그룹으로 변해간다. 과외선생이 애들을 가르치려면 4명을 맡는 것이 적당하다. 한꺼번에 다섯명을 가르치면 그 5명 중에 한 명이 애들그룹의 대장이 되어 선생에게 대항하는 수가 있다. 의사결정을 해야 하는 경우는 5명이 적당하며, 고정된 일을 반복하는 경우는 4명이 적당하며, 이심전심으로 정보를 공유하는 친밀한 그룹은 3명이 적당하다. 2명 이하는 그룹으로 보기 어렵다. 살아있는 미꾸라지를 잡으려면 다섯 손가락이 필요하다. 미꾸라지를 도망 못가게 잡고 있으려면 네 손가락이 필요하다. 죽은 미꾸라지를 이동시키려면 세 손가락으로 충분하다. 이동도 필요없다면 두 손가락으로 해결된다. 한 손가락으로는 가리킬 수 있을 뿐이다. 구조론의 점, 선, 각, 입체, 밀도는 하나의 지점에 최대 몇 개의 포지션을 집적할 수 있느냐다. 두 당구공의 접점은 한 개의 포지션이 점을 이룬다. 그 중의 하나를 회전시키면 선이 그어진다.
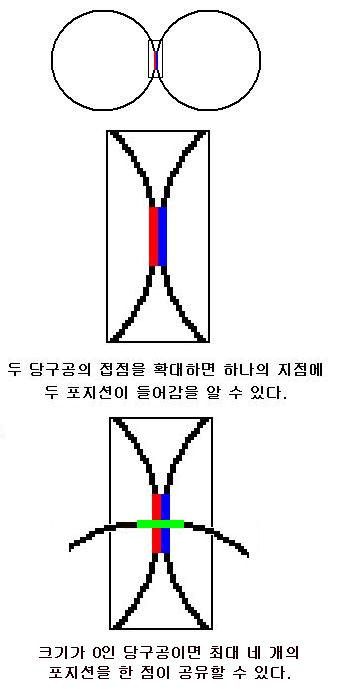
두 당구공 사이에 세 번째 당구공을 밀어넣는 것은 불가능하다. 그러나 구조론은 크기가 없으므로 가능하다. 4색이론에 따라 최대 4개까지 당구공을 밀어넣을 수 있다. 각과 입체를 이룬다.
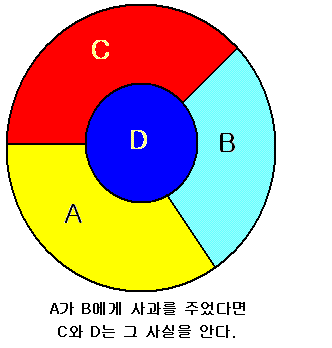
시험을 쳤는데 오늘 중에 합격여부가 통보된다고 치자. 전화가 오면 합격이고 전화가 오지 않으면 불합격이다. 이때 정보가 공유된다. 무엇인가? 불합격통보를 안 받아도 이미 받은 것이다. 구조론의 차원에서 제시되는 위상의 균일이란 일의적으로 결정되는 숫자를 나타낸다. 하나의 통보로 최대 몇 명에게 전할 수 있느냐다. 자신을 포함 전화 한 통화로 5명에게 전할 수 있다. 6명이면 실패다. 6번째 사람은 누군가의 부하로 종속되어야 한다. 여기서 계급이 만들어지는 것이다. 그러므로 계급의 발생은 구조적 필연이다. 물론 그걸로 계급제도가 정당화되는건 아니다. 시소의 원리에 따른 이심전심에 의한 자동적인 정보공유는 5명까지 가능하며 6번째 사람은 누군가에게 정보를 전해들어야 한다. 그래서 군대는 대대, 중대, 소대, 분대, 병의 편제가 생긴다. 회사는 사장, 이사, 부장, 과장, 직원이다. 봉건시대의 왕, 귀족, 사제, 평민, 농노와 같다. 지금은 왕 대신 재벌, 귀족대신 상류층, 사제 대신 전문직, 평민 대신 중산층, 농노 대신 하층민이다. 이메일을 보내거나 방송으로 통보하면 100만명에게 동시에 정보를 전할 수 있다. 그러나 이건 다른 거고 구조론은 위상의 균일에 따른 일의적인 정보공유를 논한다. 말 안해도 아는 거다. 삼총사가 되면 말로 전하지 않아도 이미 아는 거다. 우선 정보를 전하는 송신자는 알고 있다. 정보를 전달받는 수신자는 결국 알게된다. 송신자와 수신자가 두 당구공의 접점을 이루는 것이다. 엘리베이터 안에 두 사람이 있다고 치자. 방귀냄새가 난다. 누가 방귀를 뀌었지? 나는 방귀를 뀌지 않았다. 그렇다면 네가 뀐 거다. 벤치에 세 명이 앉아있는데 나는 가운데 자리에 앉아있다. 왼쪽넘이 사과를 먹고 있다. 그렇다면? 오른쪽넘이 준 거다. 맨 오른쪽 사람이 맨 왼쪽 사람에게 사과를 주면 가운데 사람은 어떻게든 눈치를 챈다. 이는 4색이론으로 입증할 수 있다. 정보의 완전한 공유는 3명까지만 가능하다. 네명이면? 정보가 내부에서 발생할 경우에만 공유된다. 만약 정보가 내부의 누군가에게서 성립하여 다시 내부의 누군가에게로 빠져나간다면? 다섯 명 중의 두 사람이 정보의 입출력을 담당하면? 나머지 3명은 정보를 공유하고 두명은 입출력하므로 5명 모두 정보공유가 가능하다. 그 이상은 마이크와 이메일과 회의를 해야 한다. 정보공유의 최대숫자는 5이며 움직이는 밀도의 장에서 성립하고 고정된 장에서는 4명이며, 일의 진행에 따라 그 숫자는 3, 2, 1로 줄어든다. 밥을 먹으러 가는 일행은 정보를 공유한다. ◎ 밥먹기 전 - 갑을식당으로 간다는 정보를 공유한다. ◎ 밥먹은 뒤 – 배가 부른지는 혼자만 안다. 밥을 다 먹어버리면 정보는 공유되지 않는다. 일의 최종단계에 도달하면 당사자만 결과를 알게 된다.
|
