
제논의 궤변 제논의 역설을 해석하고 증명하는 것은 수학자들의 관심사이고 구조론에서는 다른 이야기를 하고 있다. 아킬레스와 거북이가 경주를 하는게 아니고 '아킬레스와 거북이 사이'라는 넘이 작아지기가 있는 것이다. 괴상한 넘인데 1초에 1/2씩 작아진다. 문제는 시간도 1/2씩 줄어든다는 거다. 1초가 지나면 거리가 1/2이 되어 있다. 추가로 1/2초가 지나면 애초의 1/4이 되어 있다. 다시 1/4초가 지나면 1/8이 되어 있다. 여기서 시간은 절대 2초가 될 수 없다. 이 패턴을 반복하면 2초가 되기 전에 아킬레스와 거북이는 우주에서 가장 짧은 시간 동안 우주에서 가장 짧은 거리가 된다. 수학자들은 0.99999...=1이라고 증명해 놨다. 0.999와 1 사이에는 0.00000...이 끼어 있다. 0.00000...=0이므로 아킬레스와 거북의 거리는 0이다. 이건 수학자들의 이야기다. 규칙을 그렇게 정해버렸다. 구조론은 다른 것을 탐색한다. 어쨌든 아킬레스와 거북이는 2가 되고 그사이라는 넘은 1이다. 아킬레스와 거북은 아킬레스와 거북 사이보다 크다. 왜? 2는 1보다 크니까. 사이는 관측자다. 제 3자가 끼어 있는 것이다. 아킬레스와 거북과 관측자의 3각대결이다. 결론은 아킬레스, 거북, 사이로 세 놈이 있는데 아킬레스와 거북은 2고, 사이는 1이며, 아킬레스+거북은 > 사이라는 것이다.
|
우리는 공간이 먼저 있고 그 공간 속의 요소요소에 물질이 침투해 있다고 생각한다. 공간을 절대로 놓고 물질을 상대로 놓는다. 제논의 궤변이 의미하는 바는 공간은 없고 둘의 수학적 관계가 공간이라는 것이다. 욕조에 물을 받아놓고 탁구공 두 개를 던져놓는다. 그 상태에서 욕조의 물을 빼면 두 탁구공은 점점 다가와서 붙어버린다. 제논의 궤변이나 욕조의 물을 빼거나 같다. 위상동형이다. 양자 간의 관계가 아니라 3자 간의 관계다. 아킬레스와 거북이의 거리가 사이와 일치할 때 시간은 정지되고 게임은 종료된다. 사이는 관측자이기도 하다. 관측자가 X라면 아킬레스와 거북 사이의 간격이 X에 도달할 때 둘은 일치한 것이다. 둘의 간격은 절대로 X보다 작을 수 없다. |








 김동렬
김동렬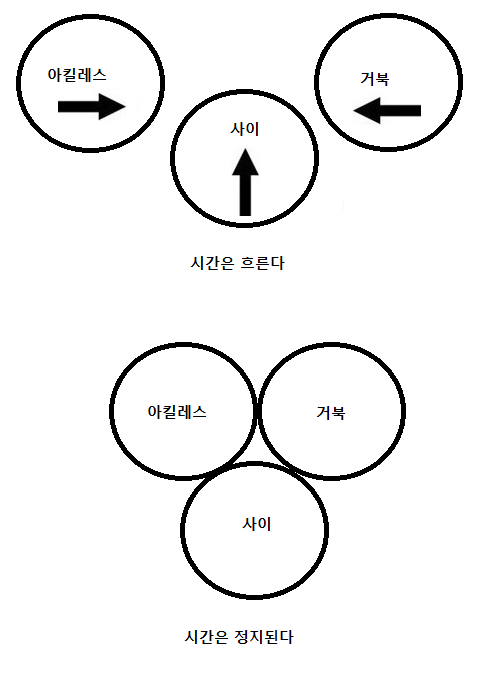





"제논의 궤변이 의미하는 바는 공간은 없고 둘의 수학적 관계가 공간이라는 것이다."
- http://gujoron.com/xe/1204387