토론실 - 다섯가지 집합

read 2601 vote 0 2020.07.28 (01:49:11)

https://gujoron.com/xe/1223101

구조론에 의하면 다섯 층위의 대칭이 있다. 집합에도 다섯 층위가 있다.

위상수학의 첫페이지에는 도넛이 나온다.

도넛의 본질은 교집합이다.

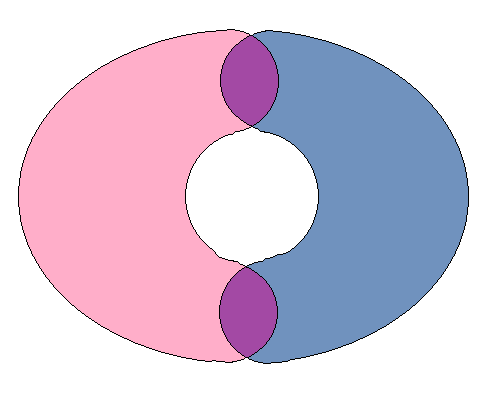
A와 B 간에 겹치는 부분이 두개 이상 존재할 수 있는 것이다.

제목 없음2.png

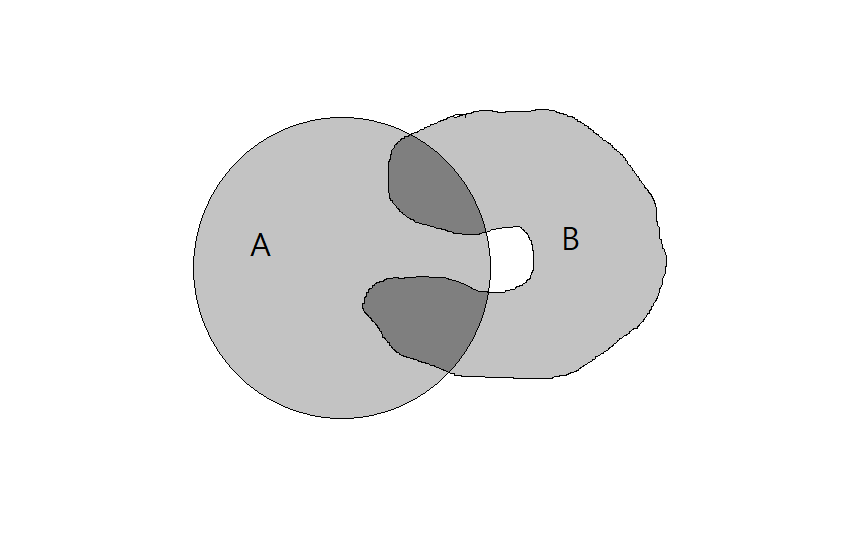
이렇게 표현할 수도 있다.

1200px-SetIntersection.svg.png

일반적인 집합론에서는 겹치는 부분을 하나만 허용한다.

제목 없음3.png

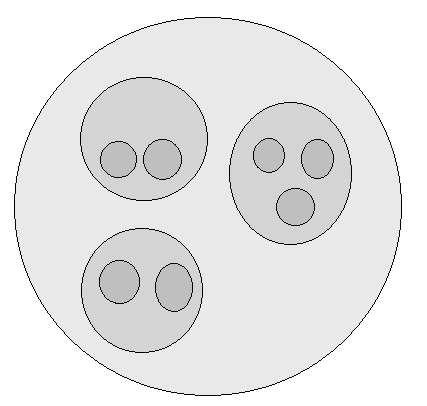
교집합을 허용하지 않고 부분집합만 허용하는 경우를 생각해볼 수 있다.

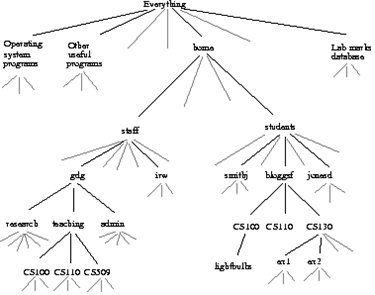
트리구조를 연상할 수 있다.

트리구조는 하나 안에 여럿이 있는 구조다. 여럿 안에 여럿이 있는 것은 교집합이다.

교집합을 허용하지 않고 부분집합만 허용하는 집합은 트리구조와 같다.

제목 없음4.png

여기서 더 나가서 집합 안에 집합이 있는 것을 허용하지 않을 수 있다.

10과 4가 있으면 6은 자동적으로 나온다. 반대로 10과 6이 있으면 4가 자동적으로 나온다. 이것이 대칭적이다.

이 대칭도 허용하지 않을 수 있다.

그러면 이렇게 된다. 원소 a로 알 수 있는 것은 a가 아닌 나머지가 존재한다는 것 뿐이다.

프린트

List of Articles

쓰기

처음 21 22 23 24 25 26 27 28 29 30 끝