
우리가 알아내려는 것은 물질의 속성이다. 그 성질은 어떤 개체에 없고 복수의 집합에 있다. 하나는 성질이 없지만 여럿이 모이면 수학적 원리에 의해 속성을 획득한다. 속성은 에너지가 방향을 바꾸는 것이며 그것은 대칭되어 나란한 2가 외력의 작용에 대해 1로 행세할 때 일어난다. 존재의 가장 단순한 형태는 두 개의 회전하는 팽이가 마주 보고 꼬여서 계를 이룬 것으로 생각할 수 있다. 하나의 팽이는 외력의 작용에 떠밀린다. 꼬여 있는 두 팽이는 세차운동을 하는 축을 움직여서 힘의 방향을 바꾼다. 두 팽이의 힘은 한 점에 전달되고 한 점이 계 전체를 대표한다. 사물은 질량과 중력과 전자기력이 꼬여서 두 개의 꼬인 팽이를 연출하고 있다. 가운데의 한 점이 코어를 이루고 계 전체를 대표한다. 그러므로 외력의 작용을 처리하여 자기 존재를 유지하는데 성공하는 것이다. 물질의 근본은 원자 알갱이가 아니라 에너지의 꼬임이다. 그것이 구조다. 정치든 경제든 사회든 문화든 이러한 본질은 유지된다. 부부 사이라도 마찬가지고 남북관계라도 마찬가지고 여야관계라도 마찬가지다. 둘이 하나를 공유하고 나란히 함께 움직인다. 그럴 때 외력의 작용에 대해 한 점이 계 전체를 대표하며 코어를 움직여 의사결정하고 외력을 처리한다.
|


https://youtu.be/olz0bNf2osQ
팽이가 쓰러지지 않는 이유라던가, 자이로스코프의 원리라던가 하는 걸 표현하는 과정에서 계를 분명히 정의할 수 있을 것 같은데, 위 유튜브 영상에서는 무중력 상태에서 자이로팽이를 돌리는 장면이 나옵니다. 무중력에서 실험하므로 우리는 중력을 무시하고 팽이를 생각해볼 수 있습니다.
우리는 보통 팽이가 쓰러지지 않는다고 생각하는데, 사실 팽이는 쓰러지지 않는게 아니라 회전 방향에 대한 자기 포지션을 유지한다고 말하는 게 더 정확합니다. 중력을 배제한다면 말이죠.
이전에 동렬님이 말씀하셨듯이 돌고있는 팽이가 세차운동을 하는 이유는 중심과 주변이 서로 돌기 때문이므로 사실 모든 단일 회전하는 물체는 두 개의 회전이 공존하는 상태라고 말할 수 있을 겁니다.
여기서 표현하기 어려운 문제는 회전의 기준입니다. 무엇에 대한 회전 포지션을 유지한다고 말할 수 없는 겁니다. 우주공간에서 자이로 팽이는 그 어떤 대상과도 분리되어있는 것처럼 보이거든요.
특히나 회전하는 자이로를 건드려도 이전 회전 축에 대한 방향을 기억하여 그 방향으로 회복한다는게 뭐라고 말로 설명하기가 어렵습니다. 대략적으로는 관성으로 설명할 수도 있을 거 같긴한데, 분명 단순한 관성과는 다른 뭔가가 있습니다.
하여간 회전하는 팽이는 무엇과도 분리되어있지만 여전히 회전을 합니다. 만약 정말 아무런 관측자가 없다면 팽이는 회전한다고 말할 수도 없을 겁니다. 그러므로 그 회전축의 기준을 말할 수 있을 때 자이로의 원리를 말할 수 있을 겁니다.
회전운동과 관성직선운동이 다른 것은 회전 운동 쪽이 뭔가 구성요소가 더 많다는 겁니다. 직선운동은 방향만 있는데 반해 회전은 중심과 주변이 있죠. 여기에 세차까지 더해지면 사실상 두 개의 회전이 공존하므로 외부 운동에 대한 독립(자기 복원 저항성)이 성립한다고 말할 수 있을 것 같습니다.
물론 모든 존재는 독립할 리가 없으므로 완전해진다는 것 자체가 사실 더 상위의 무언가에 종속됨을 의미한다고 할 수 있겠습니다. 그러므로 그것에 대해 종속하고 결과적으로 그것보다 하부의 포지션을 가지는 힘(손가락으로 건드리기와 같은 단순직선운동)에는 저항성을 가지는 거겠죠.
저는 회전하는 팽이의 상태를 그 자체를 '에너지 상태'라고 말해도 될지가 고민인데 어떻게 생각하시는지요? 즉 회전하는 팽이는 에너지에 대해 복원력을 가진다라고 말할 수 있을까요?
http://scieng.net/tech/7794
하여간 과학자들 사이에서 팽이의 원리는 여전히 미스테리라고 하네요. 어쩌면 일상에서 쉽게 접할 수 있는 팽이를 통해 중력 등 모든 힘이나 존재의 실체를 재정의할 수도 있을 것 같습니다. 보나마나 에너지의 정의를 하지 않으므로 나오는 난맥상이 아닌가 합니다.

 김동렬
김동렬
회전하는 팽이는 원심력에 의해
계가 깨져서 떨어져 나가므로 자연에 없습니다.
그러므로 두 개의 팽이가 꼬인 형태.. 실제 팽이를 생각하지 말 것..
위 그림처럼 된 구조가 우주에서 가장 단순한 구조입니다.
팽이를 또다른 팽이가 깨지지 않게 붙잡고 있는 거지요.
형태가 딱 이렇다고 생각할 이유는 없습니다.
하나는 점이고 둘은 선이며 원은 각인데
두 원이 마주보고 나란히 꼬여 있는 것을 시각화 하면 이렇다는 거지요.
원은 코어가 있고 두 원에 의해 공유되는
코어가 움직이지 않는다는 점을 나타내는 그림입니다.
끈으로 연결된 두 마리 토끼라고 해도 상관없겠지요.

원이 각이므로 하나의 회전하는 팽이는 사실상 두개의 원이 꼬인 것과 위상동형이라고 말할 수 있겠습니다. 하나의 원이 회전하더라도 실제로는 중심과 주변의 두 원이 회전하는 것입니다.
하여간 명왕성과 카론은 딱히 토끼처럼 끈이 없는데도 떨어지지 않는 것은, 그 끈이 팽이 바깥에 있기 때문이겠죠. 물론 그 끈은 우리 눈에는 보이지 않을 테고요.
잘모르는 물리학을 무식하게 끌어들이자면 맥스웰방정식에서 사원수와 외적이 쓰인다고 하던데, 외적은 두 벡터가 꼬여서 제 3의 직교 벡터를 이끌어내는 것이고, 물리학에서는 그걸 힘이라고 말합니다. 각운동량보존법칙이라고 하는것 같고요. 쿨롱의 법칙이니 하면서 오른손법칙 써서 전류의 방향 계산하던 바로 그것입니다.
물리학의 모든 보존법칙은 사실 보존이 아니라 보지않는 제 3의 존재에 대한 밸런스법칙이라고 해야 합니다.
자이로가 쓰러지지 않는 것도 이렇게 해석할 수 있으며, 눈에 안 보이는 외부의 어떤 것은 공간이라고 할 수도 있겠지만 암흑에너지라고 말할 수도 있겠죠. 이름이야 뭘 갖다 붙여도 상관없고.
다시 봐도 토끼는 좀.


 김동렬
김동렬
원자론을 대체하는
이미지를 머리 속에 그려야 합니다.
토끼가 토끼인 이유는 점프하기 때문입니다.
어떤 것이 점프하는 것이 아니라 점프가 어떤 것입니다.
움직이는 둘이 하나로 엮여 있다는 말씀.
구조는 그냥 엮인 것이고 계는 각자 움직이는 둘의 나란한 엮임입니다.
물레방아가 돌아간다면 물의 움직임과 방아의 움직임으로 두 개가 나란히 작동합니다.
즉 두 마리 토끼가 팔짝팔짝 뛰고 있다는 거지요.
물레방아를 보고도 뛰어다니는 두 마리 토끼가 안 보인다는 사람과는 대화할 필요가 없지요.
컴퓨터를 봐도 하드웨어의 작동과 소프트웨어의 작동이 있는 것이며
팔을 움직여도 에너지의 작동과 뼈대의 작동이 있습니다.
팽이가 돌고 있다면 보이지 않게 반대쪽으로 도는게 있습니다.
그것이 팽이가 원심력으로 깨지지 않게 붙잡는 힘입니다.
두 개의 팽이는 그것을 가시적으로 드러낸 것이고
한 개의 팽이가 돌고 있어도 보이지 않게 하나가 숨어 있습니다.







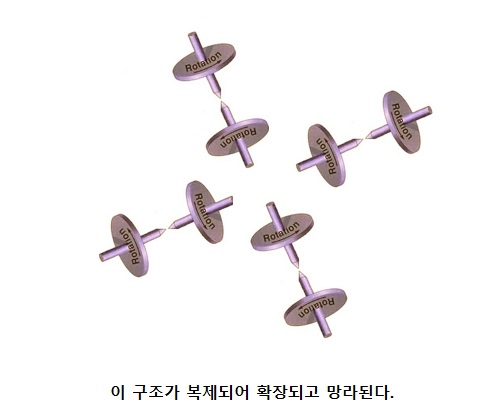





"둘이 하나를 공유하고 나란히 함께 움직인다. 그럴 때 외력의 작용에 대해 한 점이 계 전체를 대표하며 코어를 움직여 의사결정하고 외력을 처리한다."
- http://gujoron.com/xe/1195508