위의 그림을 지렛대의 원리에 의해서 풀어 본다면,
지렛대는 시소와 같은 원리이므로,
시소가 대칭을 이루기 위해서는 축이 중앙에 있어야 하지만, 균형이 맞지 않을때는 균형을 맞추기 위해서 축을 움직여 주어야 한다.
일단은 실제가 아니라 이론상으로 셋 다 모두 건너가는 방향으로 문제를 풀어본다.
위의 그림에서 셋이 모두 건너가려면 축이 이동한다는 거
그러나 축이 통나무의 길이를 벗어날수는 없다.
그렇게되면 사건이 불성립되기 때문이다.
지구의 축도 지구를 벗어날수는 없음이다.
축이 움직여 뭔가를 해결한다는 것은 그 범위가 있다.
그 범위를 파악하는 것이 먼저이다.
축을 움직이면 어디서 부터 어디까지 영향을 미치는가...이것이 전체를 보는 것이다.
이 축은 사건에서 고정되어 있다기보다 순간적으로 발생하는 경우가 많다.
그러나 축이 움직이는 것에 대하여 훈련되지 않아서 대체로 그것을 모른다.
순간적인 축의 발생은 지나가는 구경꾼도 축의 역할을 할때가 있다.
단, 축을 볼 수 있거나, 자신이 축의 역할을 해야 한다는 것을 알아차릴 때 뿐이다.
축이 움직이지 않는 사회는 변화가 없는 사회이다.
역할이 고정되어 있다고 믿는 한 축의 이동을 이해할수는 없는 것이다.
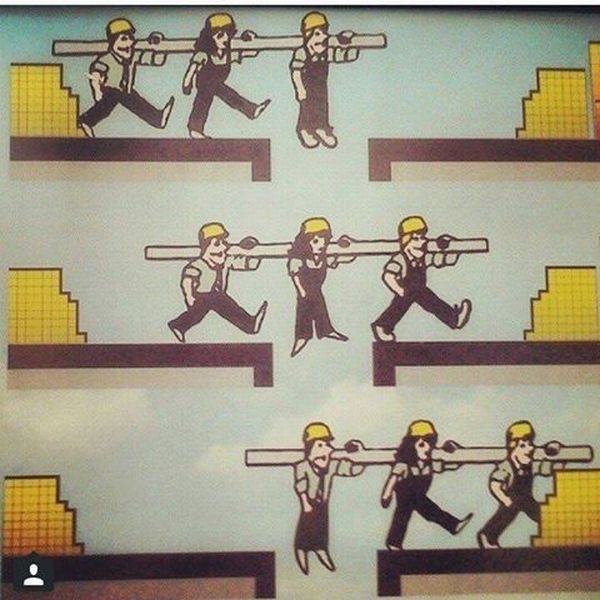
저 세 사람이 통나무를 메고 모두 건너가려면
가운데 여자아이가 움직이는 수 밖에 없다.
(편의상 그림의 좌측부터 A , B ,C 라고 하자.)
A가 건너려면 B가 A쪽으로 움직여
A와 같이 버티는 힘으로 작용해야 하며(힘의 비대칭) 이때 맨 앞의 C는 그 힘에 의해 건너가게 된다.
앞의 C가 건너가서 양쪽에서 힘의 대칭을 이루면 가운데 있는 B가 이동. B가 건너가면 다시 힘의 방향이 바뀐다(힘의 비대칭).
축의 이동으로만 모두 건너갈 수 있다. 축(B)은 건너기 전에 A쪽으로 한 번 이동해서 C를 건너게 하고, 다시 중앙으로 이동 해서 자신이 건너고, 자신이 건너고 나면 다시 C쪽으로 이동해서 A를 건너게 한다 .
이는 힘의 균일 상태를 만들어 내는 것이다.
축이 뒤로 이동(힘의 비대칭이 한번 작동) - 대칭 - 축이 앞으로 이동(힘의 비대칭이 두 번 작동)
<축이 A쪽으로 먼저 이동하는 경우>
다시 한 번 더 풀어보자.
<전제 -가설>
(저 사진에는 먼저 전제가 필요하다. 질>입자>힘>운동>량> 이라는 가설을 세우고 그대로 적용한다.
통나무를 모두 어깨에서 내려 놓지 않은 상태에서 모두 건너가야 한다.
이미 통나무를 메고 있는 세 사람이 같은 상황에 있다. 셋은 공동운명체이며 같은 계 안에 있다, 셋의 힘은 균등하다. 지구 안 이므로 중력이 작용하고 있다. 그럼으로 이 모든 것이 질의 조건이다. 입자는 통나무를 메고 있는 이들인 것이고, 이들이 다시 그 안에서 축을 움직이는 운동과 중력과 자신의 힘을 사용하는 운동을 하고 다시 실제로 그들이 거리를 이동하는 운동으로 건너간다. 이는 다시 양으로 해소 되어 처음 상태의 통나무를 메었던 원래의 포지션으로 되돌아 간다. 셋은 도랑을 모두 건넌 상태가 된다. 난관을 벗어난 것이다.)
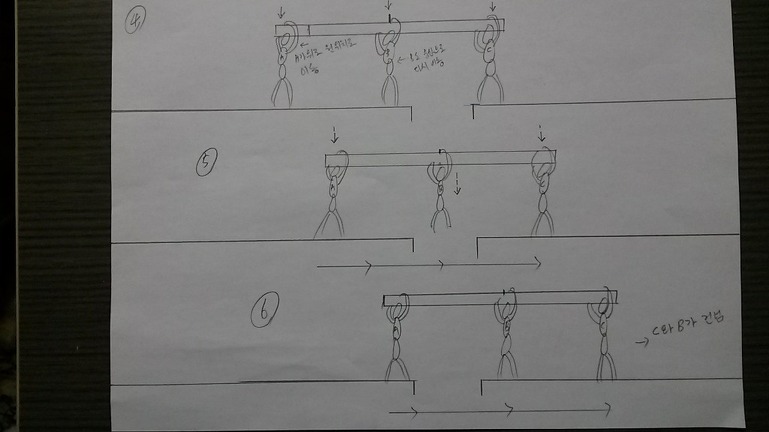
축(B)이 A쪽으로 살짝(A가 가장 힘을 쓰기에 좋은 지점, 그리고 C가 매달렸을때 수평이 되기 가장 좋은 지점) 이동하면, A가 통나무를 팔로 누르며 어깨에 지탱하는 힘과 C가 매달리는 힘이 균형을 이루어 양쪽이 서로 대칭을 이룬다. 그렇게 맨 앞의 C가 건너간다(축의 이동으로 힘의 비대칭 형성되면, A는 앞의 B(축)를 지렛데 삼아 팔로 어깨에 메고 있는 통나무를 누르며 버팀. 그러면 A의 누르며 버티는 힘과 C의 매달리는 힘이 시소의 균형 상태가 되어 수평이 회복됨- 축이 뒤로 움직여 대칭 상태를 만듬)
->
C가 도랑을 건너가서 땅에 발을 디디면, C의 매달리는 힘은 다시 버티는 힘으로 힘을 전환 시킬 수 있다. 뒷쪽의 A도 앞쪽 C가 앞에서 버텨주는 힘을 지렛데 삼아 누르는 힘 상태에서 버티는 힘으로 전환된다 - 이렇게 도랑을 사이에 두고 다시 양쪽의 통나무가 균형을 이뤄 수평상태가 되면 축이 다시 중앙으로 이동한다. 시소가 균형을 이뤄 대칭된 상태이다. 중앙에 축이 있으면 시소의 양쪽이 균형 상태가 되어 대칭을 이루므로 이때의 축의 힘은 제로 상태가 되어 중력과 일직선화 되므로 힘이 상쇄된다. 이때 양쪽이 균형을 이루면 축은 서서 버티나 매달리나 마찬가지이다. 시소가 양쪽에서 다시 균형을 이뤘으므로 B가 매달려 건너간다.( 이때는 축이 중앙으로 이동되어 시소의 완전 균형 상태, 완전 대칭 상태에서는 축의 힘이 제로가 됨. 비대칭 상태가 아니기 때문이다, 축의 역할이 드러나지 않는 상태이다.)
->
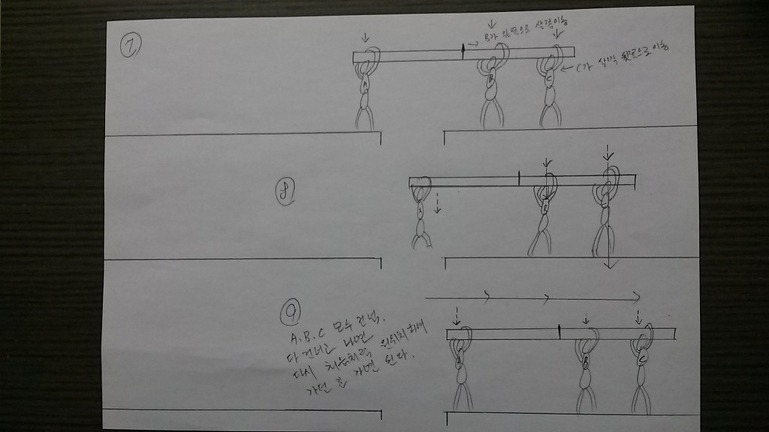
B가 건너가면 다시 축이 앞쪽인 C쪽으로 이동한다. 다시 힘의 비대칭 상태로 시소의 균형을 만든다, A가 매달려 건너오게 된다.
[ 축(B)이 A쪽으로 이동하여 힘의 비대칭 형성 - 시소의 균형을 만듬 - 비대칭으로 대칭 형성 - 축이 움직여 비대칭이 형성될때 축의 존재를 알게됨) > 시소의 완전 균형 상태 - 이때는 축이 중앙에 있어서 비대칭 상태가 아님 - 축의 힘이 제로 상태 - 일반적으로 말하는 대칭 상태 - 대칭이 눈으로 보이나 축은 안보이는 상태 > 다시 앞의 경우가 한 번 더 반복.
즉,
축 뒤로(A쪽) 이동 - 비대칭 형성- 시소의 균형으로 대칭이 한 번,
축 중앙으로 이동 - 시소의 완전 균형 - 완전 대칭으로 대칭 두 번,
축 앞쪽(C쪽)으로 이동 - 비대칭 형성 - 시소의 균형으로 대칭 세 번.
축의 이동으로
비대칭에 의한 대칭 > 완전대칭 > 비대칭에 의한 대칭
이렇게 총 세 번의 대칭이 만들어져야 건너갈 수 있음.
이것을 다른 상황들에 적용한다 할지라도...
축이 움직여야 뭔가 새로운 힘(비대칭에 의해 다시 대칭이 만들어짐)이 나오고, 또 완전한 대칭(축이 힘을 사용하지 않는 상태)을 이루려면 축이 움직이지 말아야 한다. 이것은 상황에 맞춰져야 하는 것이므로 곧 판단인 것이다.
이 문제에서 어디가 전진방향을 일으키느냐 하는 것이다.
이 문제의 엔진은 뒷쪽 그러니까 A쪽이라는 것이다.
왜냐하면, 곧 C에서는 매달려 도랑을 건너므로 자기힘으로 중력을 사용하는 것이 아니라, 다른 사람의 힘으로 사용되는 중력이 통나무를 통해서 전달되는 그 힘에 자기가 매달려 가기 때문에, 자기가 중력에 미치는 힘은 상쇄되기 때문이다. 중력을 버티고 자기힘으로 땅바닥을 밀쳐내면서 추진하는 것은 A쪽이다. 그러므로 힘을 받는 쪽으로 B가 움직여야 A와 한몸처럼 힘을 쓸 수 있고, C가 3의 힘으로 매달린다고 했을때, A가 2의 힘을 쓰고 B가 1의 힘으로 버티고, 그래야 축이 무너지지 않으므로 A가 건널 수 있는 것이라고 본다.
C가 건너려면 통나무에 매달려야 하므로, A는 어깨에 통나무를 지탱하고 통나무를 팔로 누르는 힘을 써야 하고, 이건 중력을 위에서 아래로 일직선화 하는 힘이고 또 그러면서 이동해야 하기 때문에 일직선화 된 중력에 저항하는 자기힘을 사용하며 이동해야 한다. B는 중력과 일직선화 되기는 하지만 통나무를 어깨에서 버티면서 중력에 저항하는 자기 힘으로 이동해야 한다. 이 A와 B의 중력에 저항하는 힘에 C는 매달려 건너는 것이므로, A .B .C 모두 사용하는 힘이 다르다. 힘의 쓰임이 변형된 것이다. 1단계에서 A만이 B를 지렛대 삼아 중력의 힘과 일방향이 된다. 그래서 C가 매달려도 수평을 유지할수 있는 것이다.
중력에 영향을 받을때는 자기 힘을 쓸 수 있지만,
중력의 영향을 차단하면 힘을 쓰지 못한다. 매달리기만 할 수 있다.
힘의 제로상태...상쇄되버림.(그냥 자신이 중력과 일직선화 되거나 땅에서 발을 떼어 자기힘을 사용하지 못하거나 인것은 매한가지임)
매달리거나 땅에서 발을 떼면 중력의 영향을 받지 않음. 대신 중력을 받고 있는 사람들의 힘을 이용해서 건너가면 됨.
이렇게 한 사람씩 번갈아 가며 중력의 영향을 차단하는 방식으로 이동하면 두 사람이 한몸처럼 협력하여 힘을 사용할수 있음. 축의 이동은 무게중심을 맞춰주는 것.
좌우는 무게중심을 축의 이동으로 맞춰지는 방식이 똑같고(패턴의 반복), 중앙은 좌우 수평이 될때만 이쪽으로 움직이던지 저쪽으로 움직이던지 할 수 있다.
그러므로 처음부터 앞사람을 먼저 건너게 하려면 축이 뒤로(A쪽) 움직여 무게중심을 맞추지만, 이때 앞 사람 역시 바로 매달리는게 아니라 자신이 중력의 영향을 받을때 까지는(중력에 저항하는 상태, 땅바닥에 발이 닿는 상태) 어깨에 통나무를 받치고 있어야 한다.
중력을 받고 있는 상태에서 바로 매달리면 건너기 전에 뒤에 둘이 힘이 다 빠져버려 힘을 못쓰게 됨. 이 말은 발이 공중에 뜨기 전까지는 계속 수평을 맞춰 줘야 한다는 얘기이다. 오히려 이때는 축이 뒤로(A쪽) 가 있기 때문에 앞사람(C)어깨에 얹힌 통나무 무게가 A보다 더 무겁다.
C에게 중력의 영향(중력에 저항하는 자기 힘)이 사라졌을때 뒤에서 A가 자기힘을 쓰게 되므로 C는 이 힘의 영향으로 매달려 건너갈수 있는것이다. 이때 양쪽의 무게의 밸런스가 중요하므로 타이밍이 중요하다. 타이밍을 잘 맞춰야만 중심을 잃지 않는다.
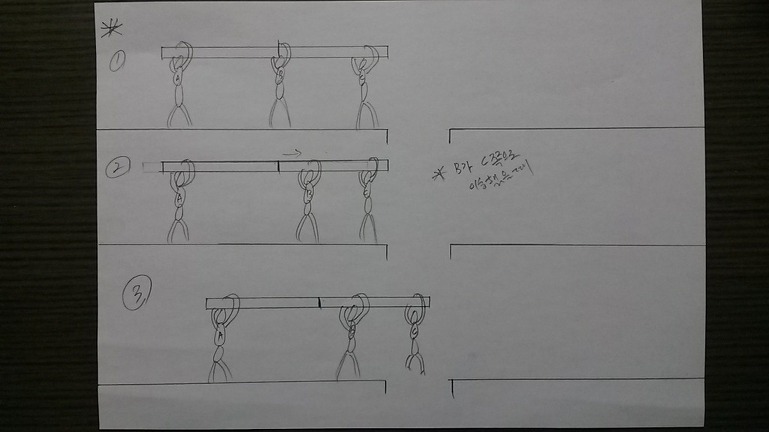
<축이 C쪽으로 먼저 이동하는 경우>
구조론은 하나를 건드려서 전체를 움직이려면 어디를 손대야 하는가라고 보는데, 이 경우라면 축에 지나치게 무리가 간다.
축이 A쪽으로 살짝 먼저 움직이면 가장 적은 힘으로 이동할수 있고, 또 축이 지렛데 역할만이 아니라 뒷사람과 같이 버티는 힘으로 두 가지로 동시에 작동 되므로 힘의 낭비가 없다고 본다. 그리고 이건 지렛대의 원리임과 동시에 시소이기도 한다. 한가지 모형에만 국한 할 수는 없다고 본다.
중력의 영향을 받는 것은 A와 B인 것이다.
C는 순간적으로 중력에 저항하여 만들어낸 A와 B의 힘을 빌어서 도랑을 건너는 것이다.
그리고 C가 도랑을 건너려면
A와 B의 이동거리만큼으로 도랑을 건너는데, 위의 사진 경우처럼 되면, B의 이동거리 확보가 어렵다.


아이참..
3이라 그래요//
건너고 싶죠?
5면 건너 갑니다.
맞아요.

흠...질은..조건... 양은 건너가 버린 것이므로 소용 없고...3이면 충분함....
중력은 이미 있는 것이고,
단지 중력에 저항하는 힘과 중력 그 자체 혹은 자기저항이 없어서 상쇄되는 그 힘을 어떻게 사용할 것인가의 문제라고 보입니다.

 김동렬
김동렬
에휴
아란도님 그림은 틀렸고요.
의심되면 직접 실험을 해보세요.
B가 C쪽으로 이동하는게 맞구요.
통나무가 짧으면 당연히 건널 수 없구요.
그러므로 교과서가 틀린 거죠.
노가다를 안해봐서 모르시는지도.

도랑 3cm로 하고, 통나무 길이를 그래서 14cm로 했음... 충분하죠.. 통나무 길이는..
그리고 제발 좀...뭐 안해봐서 모른단 말좀 하지 마세욧!!
안해봐도 선험적으로 아는게 구조론이라 하시면서..맨날 .안해봐서 모른다는 말을 달고 사시는듯...
이명박은 다해봐도 모르고
아란도님은 안해봐서 모르고
노가다 노숙이 별건가요 옛날에는 밭메다가도 애 낳다고 하는데
애낳는것과 비교하면 일도 아닙니다
글을 보면 화낼 정도의상황은 아니고 살짝 약 오르는 정도의 상황인것 같은데
뚜껑 열릴정도의 상황은 절대 아닌것 같고
약불에 살짝 부글부글 끓는 상황인것 같은 느낌인데
제머리속으로 상황이 그려지면서 웃음이 나왔습니다
저도 그런 상황 알거든요 덕분에 살짝 웃었습니다
하수들도 고수를 보고 웃을때가 있어야 공평한거 아닙니까?
아뭏튼 선험적으로 빨리 알수있기를 바랍니다 ㅎ

머~ 일단은 이렇게 넘어갑니다.
시간이 해결해 주겠지요.
이 논의에서 세사람의 체중이 동일하다는 가정이 필요합니다.
이 상태로 B가 나머지 두사람을 들어 올린 상태에서, B의 위치가 조금만 바뀌어도 한 쪽은 기울어집니다.
제가 이해 하기로는,
예를 들어, B가 조금 오른쪽으로 움직여서, 왼쪽의 A가 아래로 처진다고 해도, 동일한 체중을 가진 C가 A를 다시 들어올릴 방법은 전혀 없습니다. 오히려 C가 허공으로 뜨겠지요. C가 체중을 늘리지 않는 한은...

셋의 힘은 균등하다라고..전제 부분에 써 놨어요.

미안..
안해도 아는 것이 구조론인데..
근데 안해보면 모르는게 구조론이에요.
생각?
해보세요..그대로 되는가.

저것을 꼭 물질 상태에서만 해결 하려고 하지 말고 에너지 상태의 흐름으로 봐 보시는 것도 도움이 되겠지요.

 김동렬
김동렬
아란도님은 방송국을 찾아가서 스펀지 실험을 다시하자고 하셔야할듯.

안된다면서요...
조건이 성립이 안되서...

내가 말하고 싶은 것은..
꼭 안 건너도 된다는 것.
그걸 빼고 보라는 것.
꼭 넘어가야 되냐는 것.
못 넘어가면 어때?
씨발.

문제의 핵심은 건널 수 있느냐 없느냐가 아니라
축과 좌우 대칭의 형태를
간파해 낼 수 있느냐 하는 것.
구조론은 축, 좌, 우 이렇게 3이 아니라
거기에 2가 더 해진다는 것.

입력과 출력 부분을 얘기하시는 거자나요.
입력이 저는 A쪽으로 본다는 것이지요.
다른 분들은 C로 보는 것이고...

아제님...
저는 처음부터 건너갈 수 있다라는 전제하에서 얘기를 시작한 겁니다.
그러니 그렇게 아시고 얘기를 해 주세요.
원초적인 질문 같지만...
완벽한 균형이 맞은 상태에서 C의 발 아래 땅이 갑자기 없어지는 것 만으로도 C 가 아래로 기울어진다는 게
잘 이해가 안되네요...

누가 기울어 진다고 했나요?

그리고 제가 올린 마지막 그림에서..보자면... 어차피 C가 건너 갔으므로, 그 상태 그대로 전진해도 상관은 없겠지요. 그리고 A가 도랑 앞에 도달 했을 때 다시 C가 어깨에 맨 통나무를 더 눌러주면 되겠지요.
단, 이 경우는 C가 무사히 건넜을때 이겠지요.
결론은 C가 무사히 건너면, 그 상태는 이미, B가 건너기 전에 축(B)이 앞으로 이동된 상태이므로, 제가 말한 것으로 보면 두 번째 비대칭이 만들어진 그대로 입니다.
이리된다면, C가 건너기 전이나 후나 축인 B의 위치는 동일하다는 것이 됩니다.
그래서 동렬님 말씀을 B가 C로 이동해서 모두 건너는 것은 앞이나 뒤나 같다라는 말씀인 것이라고 여깁니다.

 김동렬
김동렬
아란도님의 착각 때문에 크레인 전복사고가 그렇게 많은 거에요.
인터넷 게시판에 크레인 전복사고 굉장히 많습니다.
전부 아란도님 책임.

ㅋㅋ... 전복사고... 그게 그렇게 되나요...
제 말은
C가 건너고 나면, 제가 말한 두번째 비대칭 상황과 동일하다는 것입니다.
그것을 얘기하고 있는 겁니다.
방법이 전과 후가 다르므로... 그 부분을 여쭙는 거지요.

구조는...
솔직히 다 알아.
대체 뭔소리야.
다 알자나..
그냥 알자나..
몰라?
모르면 어케 살았남?
물론 ..
설명을 잘해보자..이건 남았지..
그래 싸워보자..
언 넘이 잘 싸우는지..

ㅋㅋ..왜 그러시는지...?
좀 얘기 좀 해보면 안되요...?

 김동렬
김동렬

크레인이 왜 전복될까요?
전부 아란도님 생각처럼 착각한 겁니다.
아란도님 말씀이 맞다면 크레인은 절대 전복되지 않습니다.
이게 무게가 장난이 아니거든요.
수백톤이라도 자빠져요.

중심이 안맞아서 전복된다는 얘기이신데...
그렇다면, 저 앞 사다리처럼 생긴 것이 무거워서 인데... 뒤에 무게 중심이 더 있어야 하는거 아닌가요?

좀 묻지말고..해보라구..
사랑..
연애..
건축..
해보라구..
그때 물어야지..

아제님아..빠지숑...
남은 진지하게 묻는데..왜 그러는거요...도대체...

아르키메데스는 충분히 긴 막대가 있으면 자신이 지구를 들어보일 수 있다고 했습니다.
축을 기준으로 먼 쪽에서의 아주 약한 힘도
축 바로 뒤 건너편에서는 엄청난 힘을 발휘한다는 의미입니다.

이건 장도리로 못을 뽑아봐도 금방 알 수 있는 문제입니다.

구조론..원론을 말하는 거야..
실제 ..해보면..안돼..
구조론은..해본 사람이 말하는 거야..
물론 참고해..참고..
노자에...그런 말이 있더만..
천지불인..
내가 해석하면..그런거야..
구조론은...그런 것이라고 보고한거야.
근데..참..잘 봤어..
더 잘본놈이..너야?

나한테 하는 얘기요...?

아니/미안..
호롱이에게 하는 이야기야.

그럼..거기다 댓글 다세요.

그러니까... 버티는 힘과 매달리는 힘이 균형을 이루려면, 아무래도 매달리는 힘이 더 무겁지요. 왜냐, 매달리기만 할뿐 버티는데 힘을 보태는게 아니므로...
그래서, 축이 버티는 힘 쪽으로 더 이동해야 한다는게 제 생각인데, 모두 그게 아니라 매달리는 쪽으로 축이 이동해야 한다고 하니까... 그 부분이 정확히 이해가 안되므로 묻는 것입니다.
장도리도 버티는 힘 쪽으로 축이 가까이에 있는 거 맞고, 지렛대도 그렇지요.
하지만 저 건너는 문제는 반드시 수평이 맞아야 하므로, 저기도 저게 축이 C쪽으로 이동해야 하는 것이 과연 맞는가? 하는 문제제기를 해본 겁니다.

버틴다, 매달린다 이런 관점이 아니라 순수한 힘의 크기로만 생각해야 합니다.
즉 축이 가운데 있으면 좌, 우가 모두 같이 힘이어야 균형을 이룹니다.
그런데 축이 한 쪽으로 가버린다면?
축을 기준으로 먼 쪽에서는 가벼운 것이 있어도 균형을 이룹니다.
균형을 이룬 상태에서는 약간의 힘이 더 추가 되어도
한 쪽으로 쏠립니다.
못이 나무에 박히면 인력으로 뽑기는 매우 어렵습니다.
그런데 장도리의 경우 ㄱ으로 꺽인 부분이 축이 되고
축에서 가까운 부분에 못이 걸립니다.
그러면 축에서 먼 쪽에서는 많은 힘을 들이지 않고도
못이 빠집니다.

장도리의 손잡는 부분이 길쭉한 이유,
병따게의 손잡는 부분이 길쭉한 이유,
모두 같습니다.
적은 힘을 사용하기 위한 것이지요.

휴...
그러니까...
저는 축이 A로 이동하는게 장도리로 따지면 축에 더 가까우므로, A가 힘을 조금만 쓰고도 , 또 축도 힘을 덜 들이고,
C를 건너게 할 수 있다는 얘기고, 다시 B가 중앙으로 이동하면 좌우 대칭이 만들어지므로 축의 힘이 있으나 마나한 상태가 되므로(상쇄) 매달려 건너가면 되고, 또한 B가 중앙으로 이동하면 그만큼 양쪽에서 힘을 덜 들이고도 이동시킬 수가 있고,
B가 건너고 나면 다시 장도리의 축이 C쪽에 가까워져야 하므로, B가 C쪽으로 이동해야 다시 장도리처럼 축이 형성 되어 A를 건너게 할 수 있다는 얘기지요.
그리고 또, 이렇게 건너면, 모두 셋 다 모두 중력에 저항을 하지 않은 상태에서 건너가게 됩니다. 즉 자기힘을 사용하지 않고 건너는 거지요. (물론 매달리는 것도 자기 힘이긴 하죠..장도리 손잡이 부분에 아예 힘이 미치지 않는 것은 아니니까요.)
패턴의 반복이 있다는 얘깁니다. 전과 후가 같다는 거지요.
그리고 적은 힘을 들여서 모두를 이동시킬 수 있다라는 것이구요.
이것은 적용해보면, 매달려 건너는 쪽이 장도리의 손잡이 부분이거든요.
축의 힘을 이용해서 못을 빼는 거니까요.
그리고 장도리 축도 못을 뽑을 수 있는 곳에 가까이 있어서 가장 힘을 받는 것이고, 그래서 장도리 축도 오히려 적은 힘으로 못을 뽑게되는 거구요.
그리고 이 방법을 반드시 기술이 아니라도 다른 곳에 사용할 수 있다라는 것이구요.
그러나...이쯤에서 그만합니다.
대충 나올 얘기는 다 나온거 같으니까요.
그리고 저도 더 생각해 보기로 하지요.
모두 감사드려요.

축..그래 축인데..
구조론은 축..이야기야..
축을 잡아.
축이 중심인데..중심이 어디지?
그게 헷갈리는 모양인데..
중심..그게 질이지..
알고보면..중심이 질이야..
........
솔직히 말하면..세명으로 건너가지 못해.
3은 맞는데..세명은 아니야..
차라리 혼자 건너야지..
한 오백킬로..책임을 지고...
그래..배짱있지..
근데 해볼래? 되나?
인간을 실망시키려 하는 말이 아니고..
구조가..그렇다고..
1.셋이 들만 한 무게의 통나무라면 지렛대 원리고 뭐고 절대 셋이서 못 건넘. 그냥 가는 봉이라면 혹 모를까 통나무라면 길이가 늘어날 수록 무게도 늘어나니까.
2.그냥 가볍고 단단한 봉이라고 하더라도 아란도님 방식으론 못 건넘. 왜냐하면,
3.지렛대 원리를 이용하자는 건 축이 되는 사람이 천하장사가 아니라서 나머지 두 사람을 다 들 수 없어서인데, 아란도처럼 축이 뒤쪽으로 가면 결국 양쪽 두 살람 무게가 고스란히 축에게 쏠리므로 굳이 축을 옮길 필요조차 없어짐.
4.뒤쪽의 길이를 늘려서 자연스럽게 축이 앞쪽으로 가야지만 뒷사람이 매달리지 않고도, 즉 적은 힘으로도 앞 사람을 들 수 있슴.
5.그렇게 되면 축이 되는 사람이 두 사람의 몸무게를 백 프로 감당하지 않아도 되므로
6.축이 되는 사람이 그나마 낑낑대면서 몇 발자국 걸어갈 수 있슴.
7.축이 되는 사람이 걸어갈 공간이 없다는 아란도님 말씀은 역시 봉의 전체 길이를 조절하면 되므로 문제 안 됨.
에고에고 핸펀으로 타자 치기 힘드넹^^

ㅋㅋ...그렇다치구요...
앞 사람은 그렇다 치고,,그럼 맨 뒷 사람은 어떻게 건너게 하려구요...
제 방법이 틀렸다면...
앞사람 건너는 방법은 장대길이부터 별 얘기가 다 나오고 하는데,
그럼 일단 건너갔다치고, 그럼 뒷 사람은 그때부터 장도리 대입하여 축에 가까우니 그 방법으로 건너면 된다 이 얘기요...?
내 말은 얼버무리지 말고 얘기를 해보란 얘기요.
결론이 못건넌다가 아니고...
어차피 이론이고 한 번 건네보자라는 얘긴데...
저건 장도리를 예를 들었으니까..거기에 대입한다쳐도, 장도리 방식을 이쪽에 한 번 저쪽에한 번..두 번 대입하면 되는 얘기인데...
아란도님 좋은 저녁 되세요.

그러지요..계면쩍을 필요가 있을까요...
하루이틀 계면쩍은 것도 아니고...
어쨌든 제대로 알게되면 속은 시원 하겠지요.
좋은 저녁 되세요.
얼버무리는 거 전혀 아닌데요. 허허.

어떻게 똑 같냐는 거죠...
얘기하는 방식이 처음과 나중이 다른데...

난....포기한거 아닌데...ㅋㅋ^^;
단지 한번 밀어부쳐 보는 것입니다. 동렬님도 늘 그것을 바랬으므로....
좀 더 미학적 접근과 힘의 반복이 일어나는 것은 패턴의 반복이므로,
장도리 덕에...더 확실하게 입력과 출력 부분을 알게 되었는데... 소실점은 1단계 진행시의 장도리 손잡이와 2단계 진행시의 장도리 손잡이가 정확히 도랑 가운데서
한점으로 만난다는 것입니다. 정확히 반대방향으로 이지요. 장도리 두 개가 기대고 서 있다고 보면 됩니다. 손잡이 부분에 힘을 가해 못을 빼는 부분 - 이곳이 통나무에서는 C가 매달린 지점이구요.
이러면...나한테 미쳤다고 할라나....
에효..몰라효...어차피 틀려도 그만이므로...난 갈릴레이 할테야욧.
못과 손잡이 부분...
못이 중력과 일직선화 된 힘 - A가 버티고 서 있으면 못과 같음...단지 자기 힘으로 걸어가는거....근데..여기서 철로 레일 위를 펌프질 하면서 지나가는 거 있잖소..전에 구조론 야외 모임 사진에서도 보이던데.... 매달리는 C가 펌프질 하는 역할과 같소. 장도리라면 손잡이고...그래서 가장 적은 힘으로 못을 뽑고, 레일위를 달리는 거고, 매달려 건널수 있는 것. 그러니 A가 움직이는 것은 C가 매달려 있기 때문이고, 이는 C가 펌프질 하는 것과 같소.













글의 문맥을 손 봤는데, 손보다 보니 중력의 영향을 받는다라는 말이 문제인듯... 중력의 영향을 받는 다는 것은 곧 중력에 자기 힘으로 저항한다는 말이고, 중력에 영향을 안 받는다는 말은 중력 그 자체일 수도 있고, 중력에 자기 힘으로 저항하지 못하므로, 다른 사람의 힘을 빌린다는 의미라고 여김.
그리고 사진 안에서의 그림은 조건이 동일함. 도랑 너비나, 통나무 길이나, 이동 거리나...