
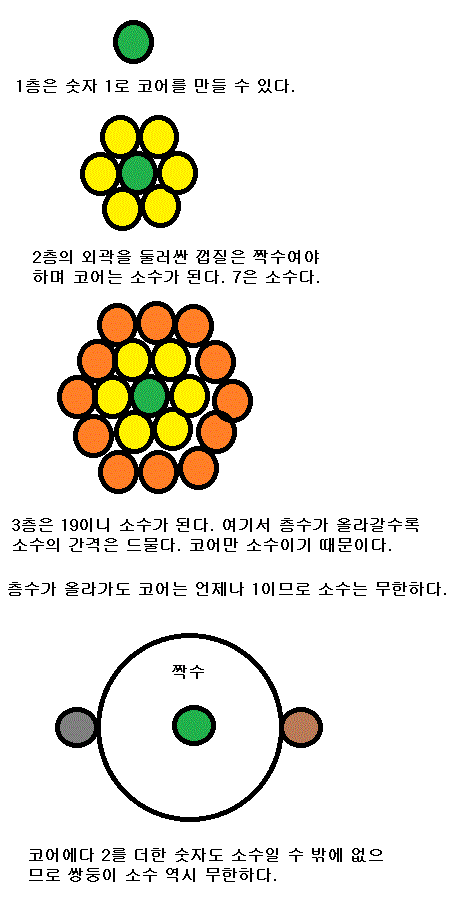
직관적 사유는 입체적 사유라 하겠다. 입체에서 한걸음 더 나아가 에너지적 사유를 얻어야 한다. 에너지의 방향성으로 세상을 바라보는 안목을 얻어야 한다. 수학을 숫자로 보면 피곤하고 물리학으로 봐야 한다. 공간의 구조로 봐야 한다. 구조론은 세상을 대칭으로 본다. 소수를 대칭의 축이 되는 코어로 생각해 보자. 소수는 대칭되지 않는 수다. 모든 소수는 홀수다. 짝이 없다. 코어는 원래 짝이 없다. 코어를 제외하고 나머지는 대칭되기 때문이다. 소수는 무한한가? 그렇다. 양파껍질의 층을 생각해보자. 양파껍질을 작은 구슬로 채운다면 껍질의 층수가 올라갈수록 많은 구슬이 필요하다. 표면적은 세제곱에 비례하기 때문이다. 코어로부터 거리가 멀어져서 층이 높아질수록 표면적이 넓어져서 더 많은 구슬이 필요하다. 그만큼 소수가 드물게 나타난다는 거다. 세제곱으로 소수가 드물게 나타나고 코어가 드물게 등장한다. 그러나 이는 입체의 표면적을 볼 때이고 반지름으로 보면 소수는 1층이 오를 때마다 같은 비율로 일정하게 등장한다. 단, 입체가 언제나 완전히 구를 이루는 대칭의 균형이어야 하는 것은 아니다. 예를 들어 소수의 곱인 11*17이라도 각각 1을 빼면 10과 16이 짝수이므로 대칭이고 나머지 1과 1이 대칭이므로 제외된다. 이런건 3초 안에 직관적으로 판단할 수 있는 것이며 과연 맞는 말인지 실제로 증명하는 것은 수학자의 일이다.
양자역학을 연구하는 물리학자와 소수를 연구하는 수학자가 우연히 서로가 같은 공식을 쓰는 것을 보고 깜짝 놀라서 합동연구를 시작했다고 한다. 양자역학이 소수의 성질을 쓰고 있다는 말이다. 그럴 수밖에 없다. 구조론적으로 보면 소수는 대칭의 축이다. 비례로 나타낼 수 없는 자투리가 코어가 된다.
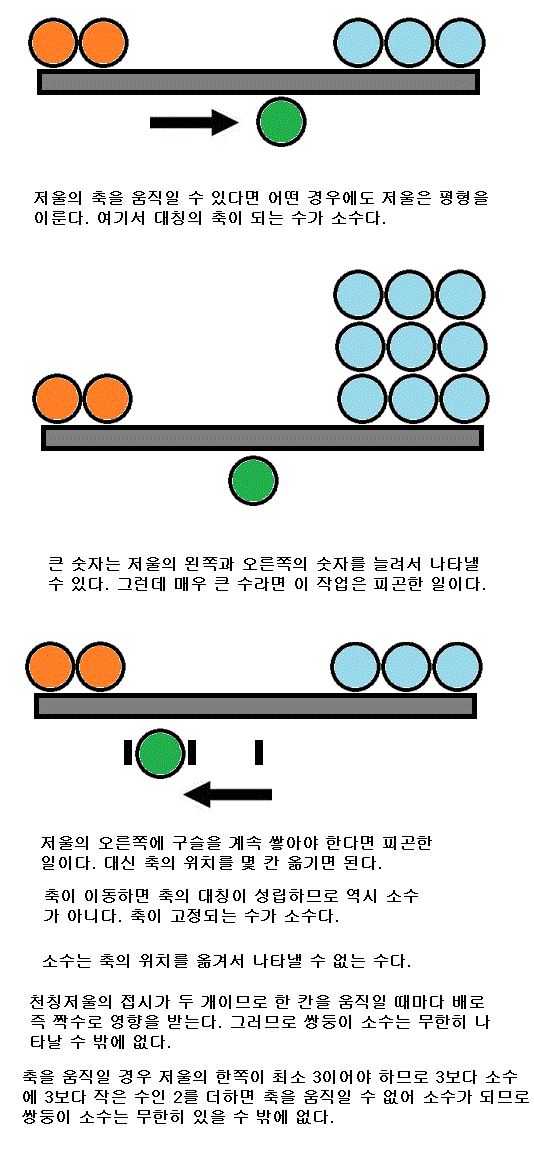
모든 수는 대칭과 대칭축의 이동으로 나타낼 수 있다.
84 = 42+42 85 = 5+5*16
|

 김동렬
김동렬
2도 코어가 있으므로 소수가 될 수 있지만 수학자들이 그렇게 정한 거지요.
저에게는 아주 흥미로운 분야라서, 그림을 보며 이해를 하려 노력해 봤습니다만 아직 깔끔하게 이해를 못하고 있습니다.
그림을 이해할 때 까지 좀 더 공부해 보겠습니다.

 김동렬
김동렬
자발적 대칭성 깨짐을 이루려면 대칭이어야 하지만 동시에 대칭이 아니어야 합니다. 그림은 모든 수를 대칭으로 나타낼 수 있다는 사실을 보이는 것입니다. 그림 그대로 저울 위에 하나씩 올리면 되며 짝수는 당연히 대칭이 되는게 저울의 양쪽에 반씩 올리면 됩니다. 홀수는 대칭이 안 되는데 대칭축에 하나를 두면 됩니다. 대칭축에 둔다는 것은 자발적 대칭성 깨짐을 일으키는 축에 둔다는 것이며 예컨대 공과 같은 둥근 물체라면 가운데 코어에 한 개를 두면 나머지 모두 채워도 정확히 대칭이 됩니다. 그래도 대칭이 안 되는 경우는 대칭축을 움직이면 대칭이 됩니다. 축을 좌우 어느 한쪽으로 이동시키는 것은 곱셈이 됩니다. 실제로 대저울로 물체를 계량할 때 추를 이동시키는 방법을 쓰잖아요.

 김동렬
김동렬
대칭적이라는 것은 맞대응이 가능하다는 의미입니다.
예컨대 남북한이 대결하는데 남한이 미국을 가지면 북한은 소련을 가지고
남한이 일본을 가지면 북한이 중국을 가지고
이렇게 맞대응할 수 있는 상황을 대칭적이라고 합니다.
맞대응이 가능하려면 짝수여야 합니다.
그런데 단 한 개는 홀수여도 맞대응이 가능합니다.
철수와 갑수가 이웃하여 사는데 위의 한국과 북한처럼 서로 하나씩 가진다고 합시다.
그런데 철수집과 갑수집 사이의 담장은 누가 가져야 할까요?
남한과 북한 사이의 휴전선은 누가 가져야 할까요?
그것은 홀수 이므로 나눠가지지 못하지만 공유가 가능합니다.
공유가 가능하므로 여전히 대칭상태를 이룬다는 말이지요.
위의 그림들은 모든 자연수가 물리적으로 대칭을 이룰 수 있음을 보입니다.
저울 위의 수는 더하면 되고 저울 아래의 수는 한쪽과 곱하면 됩니다.
어느 쪽과 곱해도 되므로 대칭적입니다.
그런데 남북한 사이의 아니
철수집과 갑수집 사이에 화장실을 공유하고 있다면
철수와 갑수는 둘 다 화장실을 사용할 수 있지만
실제로는 철수가 화장실을 쓰는 동안 갑수는 응가를 못합니다.
즉 소수는 대칭적이지만 대칭적이지 않은 숫자입니다.
구조론은 오로지 대칭을 통해서만 작동하기 때문에 자연은 대칭적이어야 합니다.
그러나 사건은 독립된 닫힌계 안에서 진행되므로 대칭적이지 않아야 합니다.
만약 대칭적이라면 질에서 입자로 넘어가지 못하고 입자에서 힘으로 넘어가지 못합니다.
자연은 소수를 통한 일정한 수학적 조건에서 즉 대칭적이면서 비대칭적인 구조에서
물질형태를 얻어 소립자를 비롯한 여러가지 형태를 만들어낸 것입니다.
만약 우주가 통째로 대칭적이라면
어떤 작용에도 상대가 동일한 정도로 맞대응하므로
모든 작용에 반작용이 동일하게 되돌아와서
힘의 방향이 확산에서 수렴으로 바뀌지 않습니다.
즉 우주는 건설되지 않고 플라즈마 상태에서 그대로 무너집니다.
중간에 코어를 두고 육각형 형태로 쌓아가는 숫자는 전부 소수는 아니지만 이런 형태의 소수는 무함합니다 ㅎㅎ
쌓아가는 형태로 소수가 아닌 숫자 중 가장 작은건 217






 17 = 6+6*2-1
17 = 6+6*2-1




이 직관적 사유와는 별 상관 없는 이야기이긴 하지만 2도 짜투리란 의미가 되겠군요