양궁국가대표가 과녁을 향해 화살을 쏘는 상황이다. 단번에 중심에 맞았을까? 맞는 것도 있고 아닌 것도 있을 것이다. 우리는 경험상 이게 자연스럽다고 생각하지만 사실은 이상한 것이다. 중앙을 노렸는데 중앙에 맞지 않는 것은 이상한 것이다. 키보드의 한 자판을 쳐보라. 근데 그게 가끔은 다른 걸로 쳐진다면? 이것은 납득할 수 없을 것이다. 요새는 잘 없지만 예전에는 누른 키가 씹히는 일도 간간히 있었다. 그렇다. 원래 사건은 의도한대로 잘 되지 않는것이 오히려 정상이다.
통계학에 큰수의법칙이라는 게 있다. 동전던지기를 해보자. 처음 몇 번은 앞면만 연속으로 나올 수도 있을 것이다. 하지만 오래 가지 않는다. 동전을 많이 던지면 던질 수록 5 : 5 로 앞면과 뒷면의 비율이 점점 같아지는 쪽으로 수렴할 것이다. 여기서 우리가 주목해야 할 것은 가끔 앞면만 연속으로 나오는 것이다.
정규분포는 큰수의법칙을 좀더 정교하게 다듬은 것이다. 큰수의법칙이 단순히 수렴성만 논한다면, 정규분포는 그 수렴을 좀더 정교하게 표현한 것이다. 동전을 열 번 던져보라. 앞면만 10번 나오는 일도 있고 앞면과 뒷면이 5 : 5로 나오는 일도 있다. 또 가끔은 1 : 9 로, 2 : 8 도 있을 것이다. 하지만 5 : 5로 나오는 일이 다른 경우에 비해 압도적으로 많다는 것을 누구나 추측할 수 있다. 그리고 이 분포 확률(또다른확률)을 그리면 정규분포가 된다. 이른바 확률의 확률이다.
동전던지기에는 두 개의 확률이 있다.
a. 앞면 또는 뒷면이 나올 확률들
b. a들이 분포하는 확률
이쯤에서 구조론의 역설을 떠올려도 좋다. 세상이 내 의도대로 되지 않는 이유는 나의 사정과, 상대의 사정, 그리고 심판의 사정이 있기 때문이다. 요즘은 오프사이드가 VAR로 좀더 정확하게 판단하지만, 여전히 재량권은 심판에 있다. 반칙을 해도 그렇다. 옥동자가 최홍만에 태클을 한들 반칙은 잘 성립되지 않는다. 최홍만에게는 그저 산들 바람이 분 것 뿐이니깐. 하지만 심판도 나름의 입장이 있다. 관중의 시선을 의식하고 상황에 맞게 판단한다.
주사위를 던져도 그렇다. 과학에서 심판은 대개 관측자로 정해진다. 윷을 던져보면 안다, 주사위와 달리 애매한 게 있다는 걸. 주사위도 스폰지 위에 던진다면 애매한 경우가 생길 수 있다. 우리가 주사위를 확정적으로 볼 수 있는 이유는 더 확정적으로 결과가 나타나도록 환경을 세팅했기 때문이다. 단단한 바닥에 던져야 한다. 원래 그렇다는 건 없다.
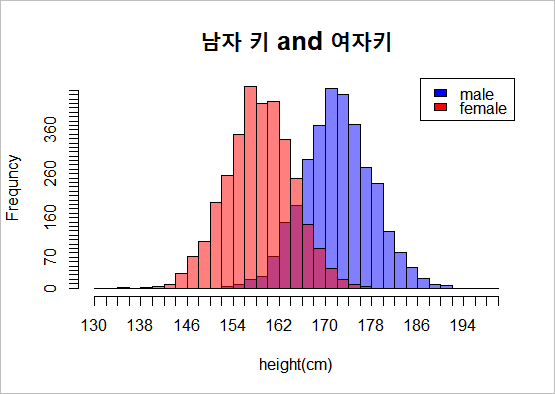
생물의 유전은 복제의 일종이며, 복제는 사건의 일종이다. 화살을 쏴도 매번 중심에 맞지 않는 것처럼, 자식도 부모와 늘 같지는 않다. 한국이 잘살게 되자 한국인의 생활 수준은 과거에 비해 우상향되었다. 국가에 돈이 돌고 의식이 풍부해져서 국민 평균의 영양상태가 좋아졌으므로 한국인의 키는 과거에 비해 많이 커진 것이 사실이다. 그런데 이게 가끔은 삑싸리가 난다. 크게 삑싸리 나면 최홍만이요, 작으면 옥동자다. 그리고 평균은 175cm이다.
내가 유치원 다닐 시절에는 흑인이 모두다 똑같이 생겼는줄 알았다. 티비를 봐도 도무지 구분이 안 된다. 초딩쯤 되어서야 흑인도 제각각이라는 것을 알았다. 외국인 눈에는 한중일인이 다 똑같아 보인다. 우리는 인디언이 낙엽을 100가지로 구분하는 것을 보고 놀라지만 인디언도 현대인이 100가지로 복잡한 세상에 사는 것을 보고 놀랄 것이다.
뭐든 그렇다. 바깥에서 보면 획일적이지만 안에서 보면 다양하다. 정규분포는 그 다양성을 수식화하고 그린 것이다. 다양하지만 모든 다양성이 똑같은 확률로 등장하지는 않는다. 한국인 키는 175에 수렴하고, 손잡이는 오른손잡이에 수렴한다. 하지만 특이한 놈들도 반드시 있다. 돌연변이도 이 맥락에서 해석할 수 있다.
최홍만과 옥동자는 유전학적으로 보면 돌연변이다. 한국인이 키가 2m가 넘는다니. 그런데 최홍만에 근접하는 사람도 꽤나 있다. 희소하지만 말이다. 돌연변이에 의미가 생기는 것은 환경이 급격하게 변하는 경우다. 운석이 날아와서 지구에 부딪치면 뜬금없이 작은 포유류가 대박을 맞는다. 공룡은 쪽박인데 말이다. 초대형인 공룡이나 초소형인 포유류나 극단적이기는 마찬가지다. 그리고 그 사이에 중간도 있다.
돌연변이는 특이한 게 아니라, 원래 그런 거다. 자연과 사건에는 오차가 반드시 있기 때문이다. 요즘은 좀 줄어들었는데, 과거에는 진화의 중심에 돌연변이가 있다는 개소리를 하는 과학자들이 꽤나 있었다. 이런 개소리를 하는 이유는 그들이 통계를 공부하지 않았기 때문이다. 무려 과학자인데 말이다. 요즘 과학자들이 논문을 쓰려면 통계를 반드시 알아야 한다. 실험을 하여 이론을 재현해야 하기 때문이다.
그런데 그 실험이 매번 100% 재현되지는 않는다. 이런 식으로 가설을 검정할 때 사용하는 도구가 정규분포의 p-value다. 가끔 실패해도 대개 맞다면 그 가설은 참이 될 수 있다는 말이다. 가설에 따라 다르다. 가설을 잘 세우면 결과에 일관성이 '대개' 있을 것이다. 100%는 아니다. 정상에서 굴러간 돌은 기슭에 모여있는게 보통이다. 그런데 가끔은 그렇지 않을 때도 있다. 재수에 재수가 없으면 그렇게 된다.

구슬을 중앙으로 쏘았으면 중앙에만 모여야 한다. 그런데 가끔은 삑사리가 난다.
https://youtu.be/-NKSDFDXuU8?t=25












