
|
에너지로 보는 관점 세상은 뼈와 살로 되어 있다. 보이는 거죽은 살이요, 보이지 않는 이면은 뼈다. 구조론은 보이지 않는 이면을 들추어 감추어진 존재의 뼈대를 드러낸다. 거죽을 보면 존재는 사물이나, 이면을 보면 존재는 사건이다. 무엇이 다른가? 시간이 다르다. 공간의 사물은 죽어있으나, 시간의 사건은 에너지를 싣고 호흡한다. 공간을 보되 시간을 보지 못한다면 존재의 절반만 본 것이다. 세상을 물질로 본다면 공간만 본 것이며 에너지로 보아야 시간을 포함한 전모가 보인다.
◎ 세상 : 물질 -> 에너지
세상은 물질이 아니라 에너지다. 존재는 사물이 아니라 사건이다. 인간은 행동이 아니라 의사결정이다. 그 의사결정은 개인이 아니라 집단의 결정이며 현재가 아니라 미래의 결정이다. 그래서 문제가 된다. 인간은 판단하고 행동한다고 믿지만 많은 경우 행동에 맞추어 변명한다. 집단은 일관성을 요구하고 시간은 연속성을 요구하기 때문이다. 우리는 무의식적으로 공간에서 집단의 영향을 받고, 시간에서 미래의 영향을 받아, 부분이 아닌 전체를 보고 결정한다.
◎ 일관성 문제 – 공간은 집단의 영향을 받는다.
인간은 사회적 동물이다. 사회라는 버스에서 운전기사의 눈치를 본다. 버스에서는 다른 사람과 보조를 맞추어야 하므로 행동의 일관성을 요구받는다. 또 그 버스는 달리고 있으므로 시간적인 연속성을 요구받는다. 승객이 버스에서 할 수 있는 행동은 제한되어 있다. 이래저래 눈치를 보다보면 어느덧 행동에 맞추어 변명하는 자신을 발견하게 된다. 기승전결로 진행되는 사건 안에서 인간은 다음 단계를 의식하고 일관성과 연속성을 지키려다가 잘못되고 만다.
◎ 공간의 해법 - 대승의 팀플레이를 통해 방향성을 얻는다.
세상이 버스라면 인간도 버스라야 한다. 대승의 팀플레이를 통해 그것은 가능하다. 조직이 치고나가는 방향성을 얻을 때 버스와 나란히 가는 대칭상태가 된다. 대칭을 통해 교착시켜 인간은 대상을 통제할 수 있다. 그럴 때 자유로이 버스에 타고내릴 수 있다. 사건은 기승전결로 전개한다. 사건의 기 단계에 개입하는 방법으로 미래를 통제할 수 있다. 버스가 출발하기 전에 자유로이 타고내릴 수 있는 것과 같다. 일단 시동이 걸리면 마이너스 개입만 가능하다. ◎ 에너지는 유체와 같아서 마이너스 제어만 가능하다. 헬륨기구는 중간에 올라탈 수는 없지만 떨어뜨릴 수는 있다. 기구가 뜨기 전에 모래와 가스를 미리 채워두었다가 공중에서 모래주머니를 던지거나 혹은 가스를 빼는 마이너스 제어로 운행한다. 이는 유체의 성질이다. 에너지의 성질은 유체와 같으며 집단의 성질과 사건의 성질 또한 유체와 같다. 유체는 마이너스로만 통제할 수 있다. 수돗물은 중간에 빠져나가는 마이너스는 있어도 채워지는 플러스는 없다. 사건이 촉발되면 돌이킬 수 없으며 마이너스만 가능하다. ◎ 유체의 성질로 시뮬레이션 하는 절차를 밟아 판단하라. 발달하는 조직, 팽창하는 자본, 성장하는 생명, 진보하는 역사는 성질이 유체와 같아서 수원지에서 수도꼭지까지 통짜덩어리로 전부 연결되어 있다. 조직을 이와 같은 구조로 편성할 때 방향성을 얻는다. 방향성이 있는 조직의 내부는 균일하게 밀도가 걸리므로 한 부분에 문제가 생겨도 조직 전체가 알게 된다. 집단에 방향성을 주는 공간의 일관성과, 사건의 초기단계에 개입하는 시간의 연속성으로 시뮬레이션 하는 절차를 거쳐 판단하면 바른 판단이 된다.
포위전이든 돌파전이든 이기는 전술의 특징은 자기편끼리의 완전한 정보공유입니다. 포위당하거나 돌파당하면 자기편을 볼 수 없어서 의사결정이 불가능해집니다. 계에 밀도가 걸리면 내부가 균일하므로 약간의 변화만 있어도 조직 전체가 알게 됩니다. 집단에 치고나가는 방향성을 주는 방법으로, 또 사건의 초기단계에 개입하는 방법으로 조직을 이 구조로 편성할 수 있으며, 어떤 판단을 할 때는 반드시 이 구조로 시뮬레이션 하는 절차를 거쳐야 합니다.
|

 김동렬
김동렬
그동안 쭉 써왔던 표현입니다.
물론 그렇긴 한데 수 많은 다른 내용과 생소한 용어들 받아 들이기 바빠서
미처 여쭙지 못하고 오랜 시간이 흘러 오늘날까지 와버렸네요.
그냥 두리뭉실하게 이해하고 있었는데 마침 오늘 글 내용에 나와서요.
사실은 더 무지몽매한 것도 있어요.
질 입자 힘 운동 량중에서 질이라는 것도 마찬가지로 모호하게 알고 있습니다.
검색도 해 보고 사전도 찾아 보았지만. 여성들의 거시기만 자꾸 나오고
아직도 긴가민가 합니다. 그냥 제1원인자 라고만 이해할뿐, 정확하게 뭔지는
아직도 모릅니다. 품질할때 질인가? 행동질할때 질인가? 암튼...
나름 이 사이트를 오래동안 들락거렸는데 이런 기초적인 것을 이해 못하다니...
그럭저럭 물어볼 시기조차 놓쳐버렸어요.

상당히 함축적인 의미를 지니고 있습니다.
제가 이해하는 것을 나열해 봅니다. 물론 평가 받고 싶은 뜻도 담겨 있습니다.
(다만, 걱정되는 것은 오히려 동렬님의 본의를 왜곡시킬지 모른다는 염려가 있어서..)
1. 어떤 상황이 더 구체화 된다.
2. 긴장이 고조가 되어 있다.
3. 변화가 될 수 밖에 없는 조건이 되었다.
4. 대칭 관계가 깨져 비대칭으로 가기 직전이다.
등등의 뜻으로 이해하고 있습니다.

 김동렬
김동렬
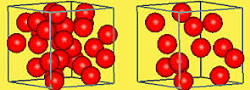
저 이미지 보고 설명 들으니 이제사 팍~ 오네요.
재미잇어서 읽고 또 읽었습니다.
이거 누군가 좀 물어봐주었으면 곁눈질로 슬쩍 하려고 했는데
유독 이 부분은 그 동안 아무도 묻지 않았습니다.
왜 이 부분이 궁금하지 않을까?
새로 들어오시는 분들도 많았는데 다들 잘 이해 하고들 있는가?
되례 한 수 가르치려 들고.. 나만 무식해서 모르나 했지요.
그런데 정말 그랬나보네요.
왜냐면 구조론 첫머리기도 하거니와 때문에 설명에 종종등장
하는데, 그러니까 더 질문하기가 민망하고 이거 물어 봤다간
바로 500방은 필수일것 같았죠.
하지만 오늘 기회를 놓치면 또 언제일지 몰라서 무식이 탄로날거
무릅쓰고 500방 맞을 각오하고 여쭈었습니다.
마침 어디 안 가시고 게시판에서 바로 방망이 날아오니 이때다
싶어 '나 이래요' 하고 자기소개를 했네요.
덕분에 이제는 어떤 사건을 구조론적으로 볼 수 있을것 같습니다.
범위를 짧게 잡으면 가족 하나에 질 입자 힘 운동 양이 다 들어
있다고 볼 수도 있겠고, 가족 외에 바깥 상황과 늘려서 1주기로
사건을 볼 수도 있겠네요.
저 때문에 설명하시느라 애쓰셨습니다.
거듭 감사드립니다.

 김동렬
김동렬
http://www.ktword.co.kr/abbr_view.php?m_temp1=4476
계에 대해서 잘 설명되어 있소.
굳이 이렇게 거창하게 들어갈 건 없고 그냥 거시기라고 해도 됨다.
네~ 먼저 설명을 듣고 아줌씨들이 좋아하는 낙찰계도 '계'겠구나 싶었습니다.
그런데 어떤 멋진 남자가 마담뚜 계주를 꼬셔서 계돈들고 튀면, 밀도와 에너지가
붕괴 되어 입자로 가지 못 하고 소멸인가요. 고 낙찰계만.. 각자는 또다른 계고..












"계에 밀도가 걸린다"는 말이 무슨 뜻인지
좀 더 자세히 알고 싶습니다. 생소한 용어는 당췌~