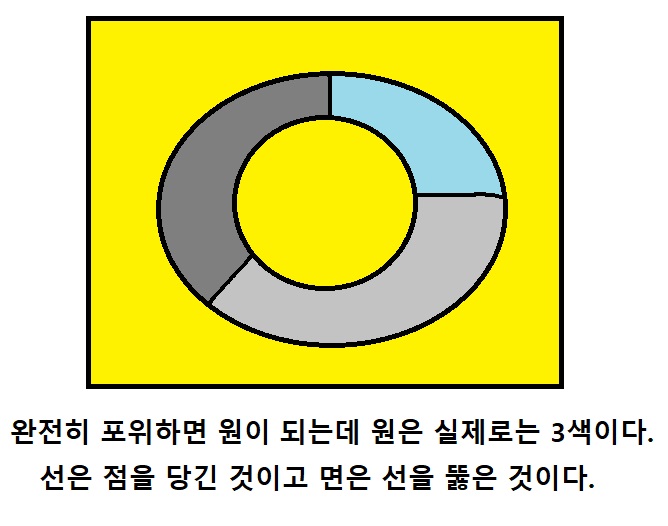
지도의 구역을 사색으로 나타낼 수 있는 이유는 한 점이 주변 세 점에 의해 내부에 갇히기 때문이다. 내부에 가두어 완전히 격리되므로 같은 색으로 칠해도 공유하는 국경선이 없이 구분된다. 면으로 된 구역을 가두려면 주변이 삼각형 이상의 다각형이 되어야 한다. 모든 닫힌 도형은 위상이 같다. 출발점과 도착점이 둘이다. 삼각형과 원은 위상이 같다. 원은 컴퍼스의 삼각형을 복제하므로 의사결정점 숫자가 같다. 삼각형의 세 점에 내부의 갇힌 점을 더하면 넷이다. 넷으로 하나의 구역이 외부와 격리되어 국경이 겹치지 않는다. 쾨니히스베르크의 일곱 다리와 정확히 같다. 한붓그리기와 사색정리가 위상동형이다. 모두 두 개의 출발역과 도착역을 가진다. 에너지의 입구와 출구가 둘이다. 합쳐서 의사결정지점이 넷이다. 한붓그리기가 증명되었으므로 위상동형인 사색정리도 증명된 셈이다. 한붓그리기는 하나의 긴 선이다. 누에가 아무리 실을 많이 뽑아도 그것은 한 가닥의 실이다. 누에의 입은 하나의 점이다. 입이 움직이면 선이다. 점을 늘여서 선을 만든다. 고무덩어리는 점이다. 고무덩어리를 잡아당기면 고무줄이 된다. 고무줄을 뚫으면 면이 된다. 덩어리의 점, 늘이기의 선, 뚫기의 면까지 3회 의사결정으로 원이나 다각형이 만들어진다. 사색정리는 사면체다. 사면체는 외부와 단절된다. 네 점을 지정하여 독립적인 공간을 만들 수 있다. 마찬가지로 하나의 구역은 국경선 셋으로 외부와 완전히 단절시킬 수 있다. 원으로 에워싸서 구역을 외부와 단절시킬 수 있지만 원은 컴퍼스의 세 지점을 정해야 성립하므로 위상동형이다. 모든 평면의 닫힌 공간은 세 지점을 지정해서 만들어진다. 원은 시작점과 도착점에 콤파스의 벌림점이 있다. 선은 시작점과 도착점이고 점은 기점이다. 한붓그리기는 하나의 점을 잡아당겨 선으로 만든다. 짝수의 교차점은 그냥 비켜간 것과 같다. ><는 네 선이 교차하지만 실제로는 >와 <이며 둘이 접촉하지 않아도 상관없다. 그러므로 네거리는 =와 같다. 그냥 선이 두 번 지나간 것이므로 펼치면 한 가닥의 긴 선으로 된다. 한붓그리기를 성공시키려면 입구와 출구는 홀수인 삼거리라야 한다. 이때 홀수 교차로는 짝수로 있어야 한다. 홀수 교차로의 숫자가 홀수로 되면 삐죽하게 혹이 튀어나온 모양이 되기 때문이다. 닫힌 도형에 팔이 하나 튀어나온 모양이다. 그것은 교차로가 아니다. 한붓그리기는 오일러에 의해 증명되었으므로 한붓그리기와 사색정리가 위상동형이라는 점만 증명하면 된다. 사색정리는 두붓그리기와 같다. 한붓그리기를 깨는 문제다. 원은 한붓으로 그릴 수 있다. 도너츠와 같다. 도너츠에 막대를 끼우면? 혹은 도너츠를 끼우면? 사슬이 된다. 사색정리는 입구와 출구가 둘씩 있다. 입구와 출구가 둘씩 있으면 한붓으로 그릴 수 없다. |







 김동렬
김동렬