
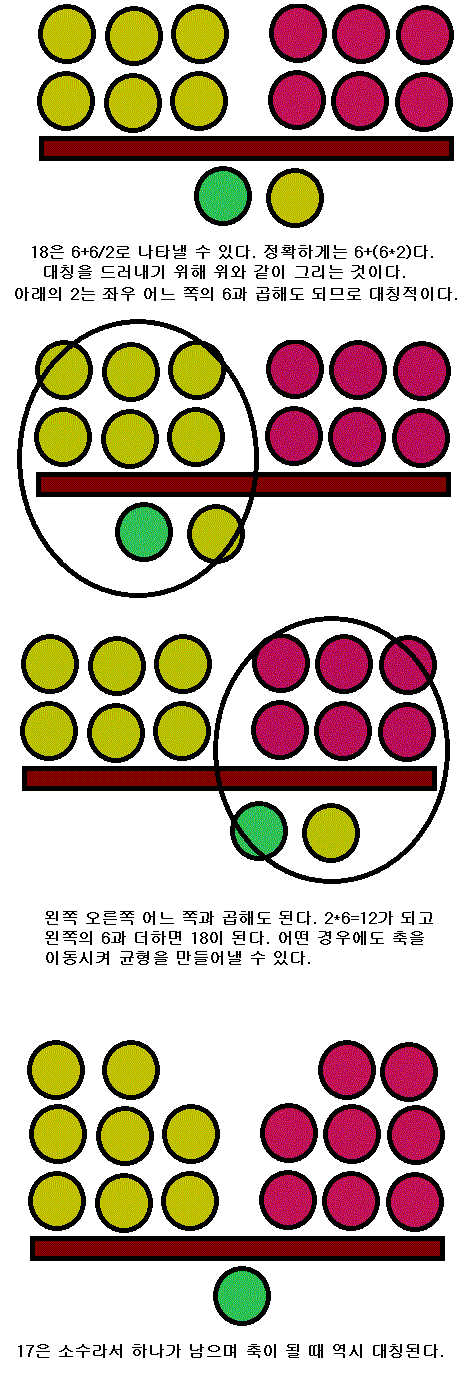
구조론은 닫힌계라는 표현을 쓰지만 자연에서 저절로 잘 안 닫힌다. 어떤 것이 있는데 에너지 작용을 가했을 때 정확히 반작용하면 닫힌계라 할 수 있다. 그런데 자연은 진흙처럼 물렁해서 힘의 작용이 잘 되돌아오지 않는다. 갑돌이를 한 대 때렸는데 금방 화를 내며 째려본다면 갑돌이의 존재는 증명된다. 그런데 열 방을 때려도 반응하지 않고 죽은 척하고 있으면 곤란하다. 반응하는 존재로 만들어야 한다. 인간이 만든 물건들은 대부분 인공적으로 심을 삽입한다. 예컨대 눈을 뭉칠 때는 손의 체온으로 눈을 살짝 녹였다가 다시 얼려 단단한 심을 만들어 눈뭉치 속에 넣는다. 별사탕은 좁쌀을 핵으로 사용한다. 인위적으로 핵을 삽입한 것이다. 과일도 핵이 없으면 형태가 짜부러진다. 청포도는 씨가 없는데 타원형이 되었다. 꽃가루받이가 안 되어 껍질만 자라다가 죽는 과일이 있는데 아마 살구종류였을 거다. 수정이 안 된 것은 모두 형태가 짜부러졌다. 점토로 석고상을 만들어도 나무와 새끼줄로 심을 만든다. 양자역학은 깊이 들어가면 수학만 남는다. 그냥 숫자다. 숫자가 어떻게 형태를 도출했지? 소수 때문이다. 소수는 과일의 핵이 되고 대칭의 심이 되고 코어가 되며 대칭을 유지하면서도 특정 조건에서 대칭을 깨뜨려 닫힌계를 이룬다. 이게 없으면 자연은 약분되고 소인수분해 되고 해가 풀려 사라진다. 휴전선을 남북한이 공유하듯이 담벼락을 이웃집과 공유하듯이 하나이면서 2의 행세를 하는 것이 있다. 평소에는 대칭을 유지하고 있지만 누가 건드리면 대칭이 깨져서 닫힌계를 만들고 안으로 버티며 외력에 대항한다. 반작용을 한다. 작용해 오는 힘의 방향을 바꾼다. 소수가 그 역할을 하는 것이다. 양은 순해서 쉽게 통제할 수 있다. 동시에 양은 순해서 통제하기 어렵다. 양은 숫자가 많기 때문이다. 양치기가 심의 역할을 하고 코어 역할을 한다. 양은 순해서 다루기 쉽고 양치기 한 명만 상대하면 되므로 에너지도 절약된다. 소수가 없다면 양치기 없는 양떼와 같아서 다루기는 쉬운데 번거롭다. 계에 외력을 작용시켰을 때 그 외력이 되돌아오는 시작점이 구조론의 특이점이다. 계는 대칭을 이루어야 자체적으로 유지된다. 대칭을 이루면 짝수라서 특이점이 없다. 반작용의 시작점을 정하지 못한다. 국가는 왕이 코어가 되고 가정은 가장이 코어가 되는데 숫자는 왕이 없으므로 코어가 없다. 숫자는 평등해서 리더가 없으므로 콩가루집안이 되는 것이다. 반작용의 시작점을 도출하지 못하면 외력에 약해서 깨진다. 다이아몬드가 강해도 사실 잘 깨진다. 다이아몬드가 유리를 이기지만 쇠망치로 치면 깨진다. 쇠는 무르지만 깨지지 않는다. 리더가 있어야 깨지지 않는 견고한 조직이 된다. 자연에서는 소수가 외력에 맞서는 반작용의 시작점이 된다. 즉 어떤 계가 소수일 때 외력에서 작용하면 반작용할 확률이 높다. 정 모르겠으면 당구공을 짝수개나 홀수개로 모아놓고 한 번 쳐봐라. 어떻게 되는지. 짝수개로 당구공을 모아놓고 때리면 공은 그냥 밀려갈 뿐 되돌아오는 힘이 약하다. 당구공을 특정한 수학적 배열로 배치했을 때 외력의 작용에 저항하는 힘이 강해진다. 벌집이 육각형을 이루듯 대칭이면 좋고 대칭구조에 핵이 있으면 더욱 좋다. 속을 비워도 빈 공간이 핵의 역할을 한다. 속에 심을 만들어 넣거나 속을 비워두면 구조는 튼튼해진다. 숫자가 소수이면 더욱 좋다. 그런데 이 분야를 연구하는 수학은 없다. 인류의 수학은 아직 원시상태를 벗어나지 못하고 있는 것이다. 구조론 없는 수학은 허수아비나 마찬가지라 하겠다. |







 김동렬
김동렬





[자연에서는 소수가 외력에 맞서 반작용을 하는 시작점이 된다.
즉 어떤 계가 소수일 때 외력에서 작용하면 반작용할 확률이 높다.
정 모르겠으면 당구공을 짝수개나 홀수개로 모아놓고 한 번 쳐봐라. 어떻게 되는지.
짝수개로 당구공을 모아놓고 때리면 공은 그냥 밀려갈 뿐 되돌아오는 힘이 약하다]
=> 신세계로 들어가는 입구이군요!