푸리에에 관해서 웹서핑을 하다 흥미로운 사이트를 발견하여 소개 하고자 합니다.
푸리에 급수가 의마하는 바가 "복잡한 파동도 단순한 파동의 합으로 표현할 수 있다." 라는 의미인데
이것을 실제 테스트 해볼 수 있는 사이트 가 있어서 테스트를 해보았습니다.
아래 그림과 같이 왼쪽 네모안에서 마우스를 이용하여 임으로 파동을 그리면 오른쪽에
해당 파동을 단순한 여러개의 파동으로 분리해서 보여줍니다.
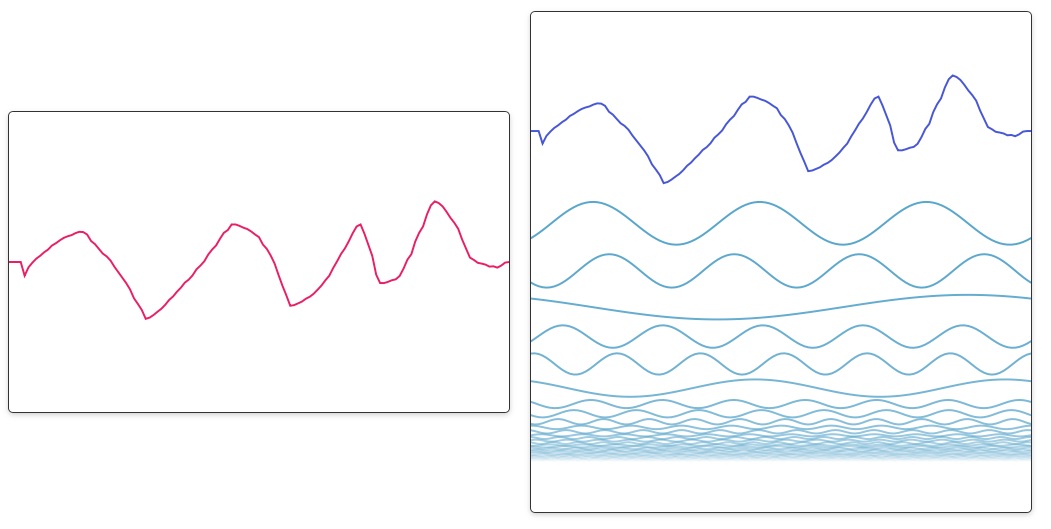
일반적으로 하나의 파동을 표현할때 아래 그림처럼 원운동을 이용하여 표현을 할 수 있게 되는데
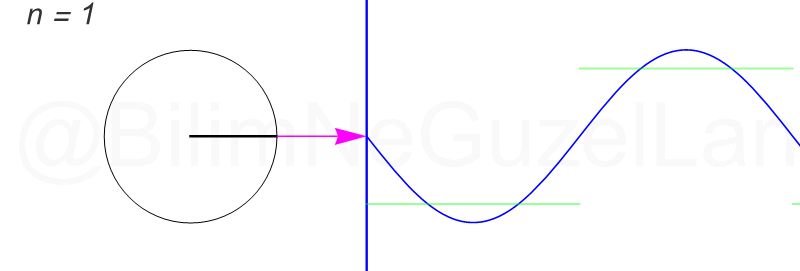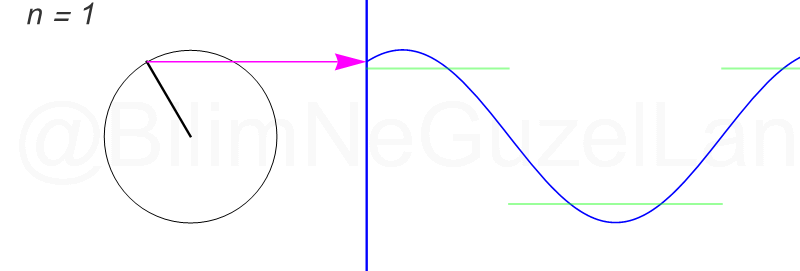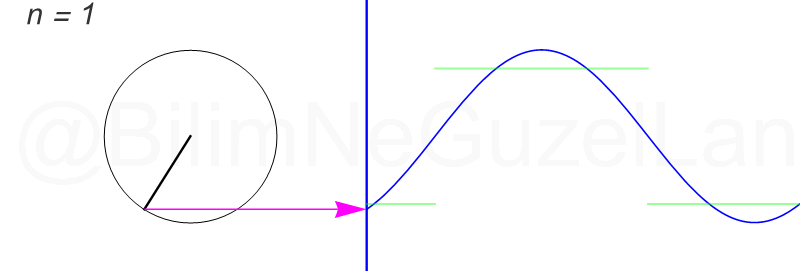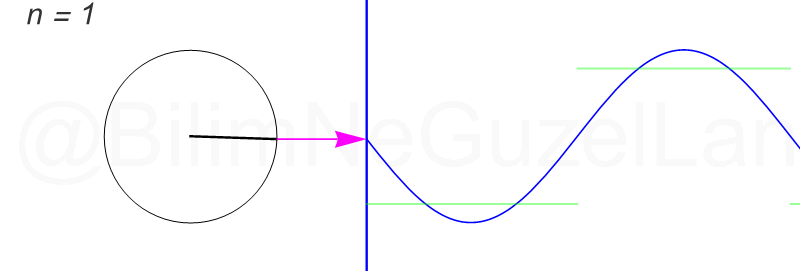
어떤 파동이 13개의 파동으로 구성이 된다면 아래 그림과 같이 13개의 원을 이용해서 표현할 수 있습니다.
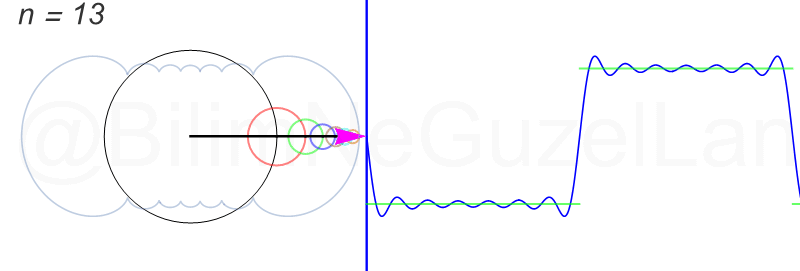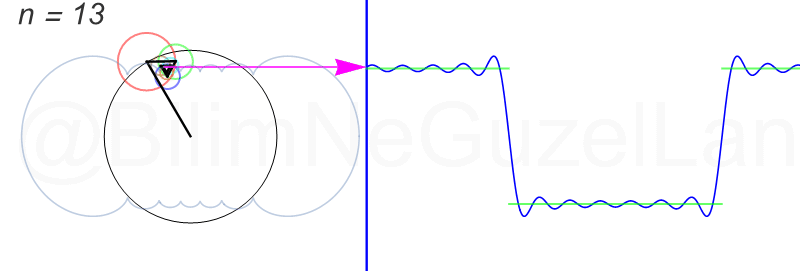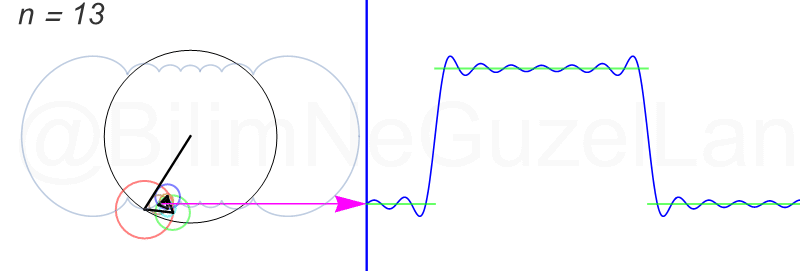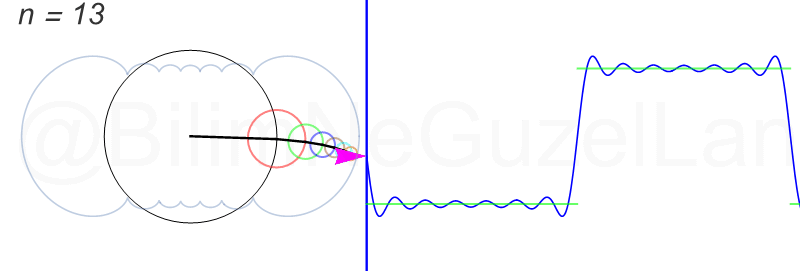
이렇듯 여러개의 원운동의 조합으로 복잡한 파동을 표현할 수 있는데
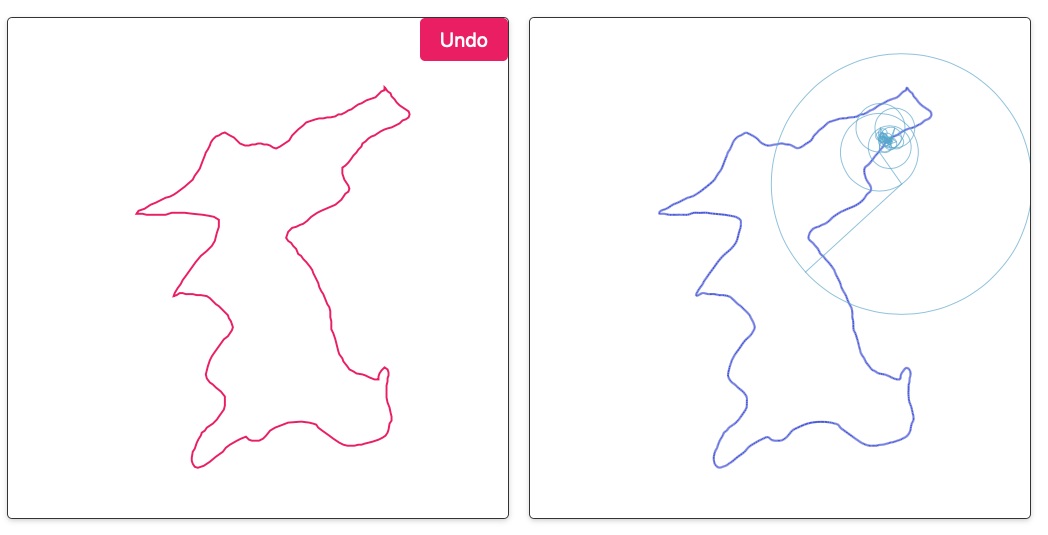
꼭 파동 형태가 아니더라도 아래 그림 같이 우리나라 지도 모양을 마우스로 그리면
수십개의 파동(원)을 이용하여 바로 표현을 해주네요. 한번 해보세요.
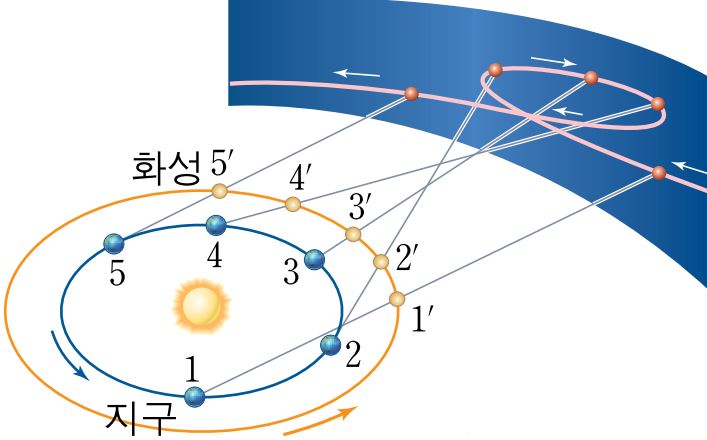
아마도 예전에 천동설을 주장하던 학자들이 태양계의 복잡한 운동을
이런식으로 계산을 해서 표현을 했겠구나 하는 생각이 드네요.
푸리에 변환 테스트 해볼수 있는 사이트
http://www.jezzamon.com/fourier/
기타 참고 사이트
http://bilimneguzellan.net/en/purrier-series-meow-and-making-images-speak/
위사이트 중간에 보면, 동영상이 하나 있는데 그 내용도 상당히 재미있습니다.
초고속 카메라로 방안에 있는 식물이나 과자 껍데기를 촬영을 한 후 식물 잎이나 과자 포장지의 미세한 떨림을 분석하여 방안에서
발생하는 소리를 거꾸로 만들어 내는 장면이 나옵니다.


머신러닝의 음성인식 분야에서 푸리에 급수는 신호의 전처리에 사용되는데(노이즈 제거), 이게 노이즈 제거만 겨우 가능할 뿐, 원 신호의 원구성까지 정확하게 재현하지는 못합니다. 그래서 주요 모델에 머신러닝을 사용하죠. 물론 머신러닝도 푸리에 급수처럼 잘 안 맞습니다.
그럼 이걸 어떻게 해결하나? 미리 정답지를 몇 개 제시하고 그 중 하나를 맞추는 객관식 문제로 바꾸는 겁니다. 즉 푸리에 급수는 주관식인데, 객관식으로 후보를 구성하여 맞출 확률을 비약적으로 높이는 거죠.
이게 최신 머신러닝이 급격히 발전한 원리입니다. 지도학습이라고 하죠. 객관식의 항은 보통 이름표(라벨)이라고 하고요.

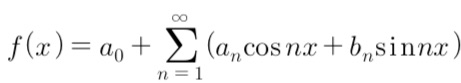
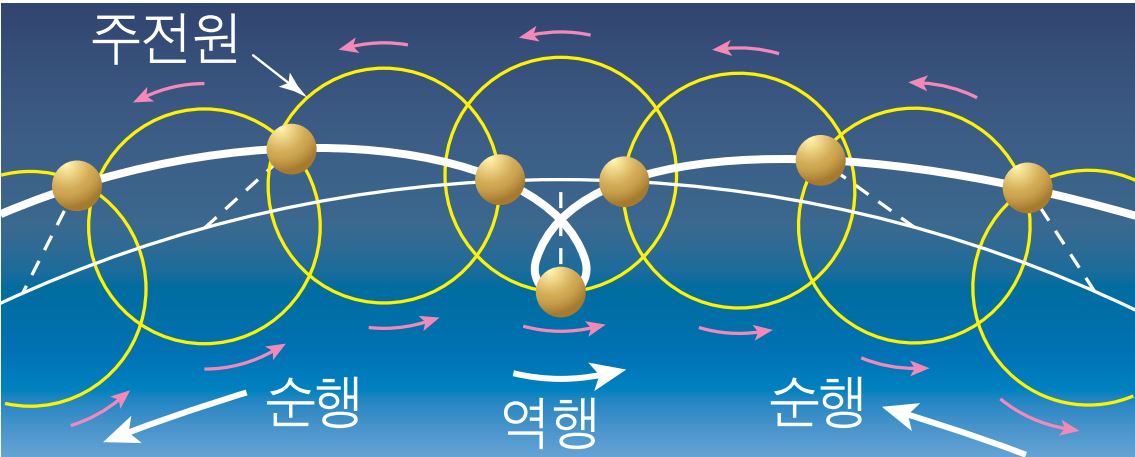

제가 주기성은 미처 확인을 못했네요. 말씀하신대로 노이즈의 기준은 주기성의 여부입니다. 주기성이 없다면 신호도 노이즈로 처리될 수 있겠죠. 거꾸로 노이즈라도 주기성이 있으면 신호로 분류됩니다. 이때 핵심은 주기의 기간인데, 기간이 너무 긴 주기를 가진 신호는 노이즈로 처리될 수 있기도 합니다. 여기에 닫힌계 개념으로 어느 정도의 주기를 가진 신호를 계 안으로 넣을 것이냐가 문제가 될 수는 있겠지만, 태양계를 한정하면 해결되므로 일단 이건 넘어가죠. 더 큰 쟁점은 따로 있습니다. 참고로 급수의 개념이 없어도 천동설은 꽤 정확했다고 합니다. 오히려 지동설이 부정확했죠.
https://namu.wiki/w/%EC%B2%9C%EB%8F%99%EC%84%A4
#
여기는 구조론연구소니깐 논의를 좀 더 확장해보죠. 제가 제기하고 싶은 것은, "과연 우리는 지구에서 우주의 진리를 알 수 있는가?"입니다. 천동설의 예에서도 보다시피 천동설이 꽤 정확한 관측값을 내놓았음에도 불구하고 인간들은 끝내 지동설을 꺼내듭니다. 천동설로도 충분한데 이럴 이유가 없잖아요. 게다가 당시엔 우주로 나가서 확인할 수도 없습니다. 반박할 수 없고, 게다가 정확하기까지 한게 천동설인데, 지동설은 도대체 왜 튀어나온 걸까요?
제 추측입니다만, 천동설은 반직관적이었기 때문일 겁니다. 천구가 저렇게 스프링처럼 돌면 뭔가 이상하잖아요. 소실점이 없기 때문에 천구가 가진 회전의 동력을 가정할 수 없는 거죠. 과학자들은 천동설을 주장하면서도 계속 찝찝했을 거라고 봅니다. https://www.youtube.com/watch?time_continue=57&v=EpSy0Lkm3zM
어떤 단계의 지식 내부에서는 맞지만 다른 지식과 연결되지 않는 대표적인 사례가 천동설입니다. 즉 보편성이 없습니다. 이는 귀납의 폐해입니다. 보통 귀납의 폐해로 백만번 맞다가도 1번만 틀리면 이론 전체가 무너진다는 식인데, 귀납의 진정한 폐해는 보편 지식과 매칭되지 않는다는 겁니다.
제가 하고 싶은 말은 이겁니다. "어떤 현상을 푸리에급수 하나로 퉁쳐서 해결할 수 없다. 추가적으로 보편 지식과 비교 검증할 필요가 있다." 이때 사용되는 게 보편적 모델입니다. 우주의 먼지인 지구의 먼지인 인간 입장에서 우주를 사유하려면 보편 모델이 필요합니다.
#
그리고 박스 안에다가 (주기없이) 임의로 선을 그었는데도 주기함수를 찾는 이유는 푸리에 "변환" 때문에 가능한 것 같네요. 푸리에 급수와 변환은 다르다고 하죠.
근데 좀 이상하긴 하죠. 주기가 없는 패턴인데 주기를 찾아낸다니. 푸리에 변환은 임의로 주기를 가정한 것 같네요.

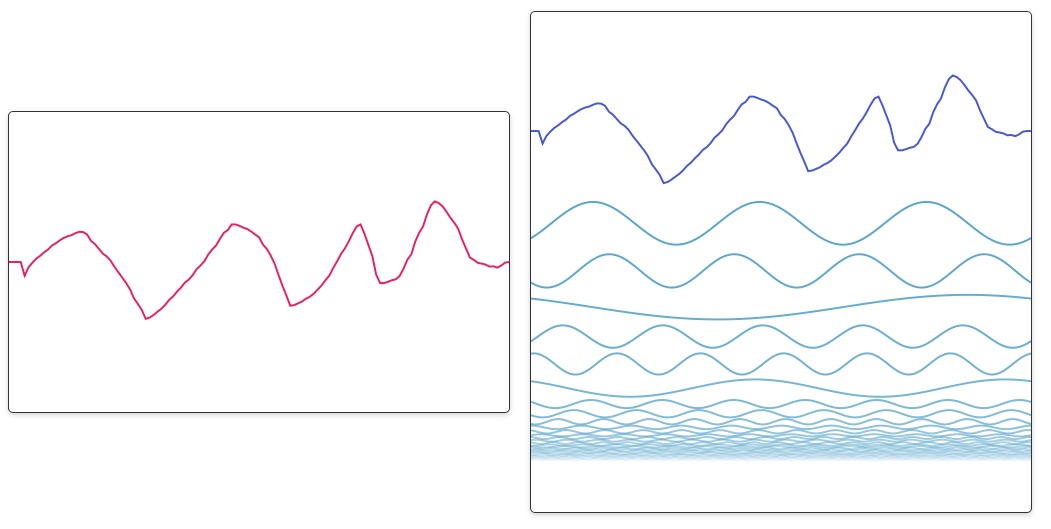

무한급수의 주기는 무한대라기 보다는, 주기를 관측한 범위, 즉 "오리님이 그려넣은것 까지만"이라고 퉁친게 아닐까 합니다.



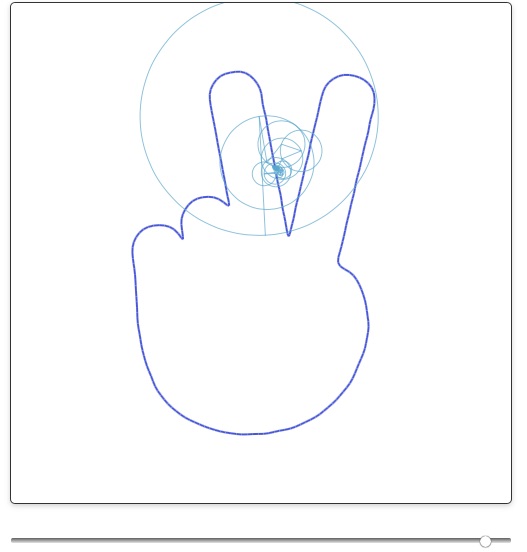

아하.
도청을 찰영한다. 와우

- 푸리에급수
- 푸리에변환
- 푸리에변환과 파동의 불확정성











