
|
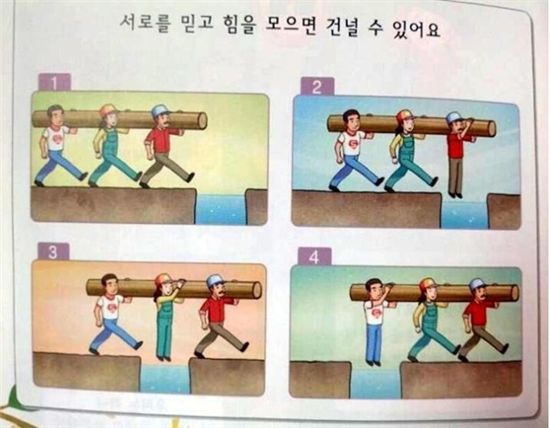
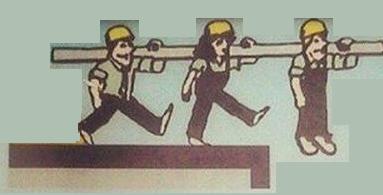
예전에 나온 이야기인데 이게 이해가 안 된다는 분이 있어서 다시 말씀드립니다. 교과서에 나온 그림이라는데, TV프로 스펀지에서 실험해보니까 실제로는 불능으로 밝혀졌다고. 그래서 올해 교과서에서는 삭제된 내용이겠고.
아마 이게 원본 그림이고 맨 위의 그림은 한국의 교과서가 몰래 표절한 모양인데, 작업할 때는 안전모를 써야 하므로 한국의 교과서는 공사장 안전수칙 위반입니다. 어쩌면 경범죄에 해당할지도. 안전모 흰색은 감독, 노란색은 노동자입니다. 이 그림을 보면 한국사회가 얼마나 노동자의 목숨을 경시하는지 알 수 있습니다. 공사장에서 일 시키면서 안전모도 지급하지 않다니. 심지어 정부에서 하는 공사인데도. 두 번째 컷을 봅시다.
이게 지렛대지 않습니까? 동시에 시소이기도 하고, 천칭이기도 하고, 세상의 모든 구조는 같습니다. 그러니까 이걸 볼펜이라고 해도 되고, 식칼이라도 해도 되고, 피리라고 해도 됩니다. 우주 안에 다른 구조는 없어요. 세상에 오직 구조는 하나 뿐. 이건 필수암기 사항입니다. 여기서 소실점과 대칭이 다 보이죠? 그렇죠? 이게 보여야 합니다. 예외는 없으니깐. 대칭도 있고 소실점도 있네요. 딱 있잖아요. 보이죠? 미켈란젤로의 천지창조에서 아담과 하느님의 손끝이 보입니까?
자 두 번째 컷이 이 구조입니다. 가운데 축을 맡은 여자가 양쪽의 두 남자를 메고 있습니다. 여자 한 사람이 건장한 두 남자와 통나무 포함 도합 200키로를 짊어지고 있어요. 대단하죠. 아마 역도선수 출신일 겁니다.
다시 보세요. 여기서 오른쪽 빨간티 입고 하얀모자 쓴 남자가 여자를 지렛대의 축으로 만들어서 맨 뒤에 오는 남자를 공중부양 시키고 있습니다. 정 이해가 안되면 직접 통나무 들어보세요. 에구 그냥 손가락에 볼펜을 올려보세요.
이런 구조로 되어 있습니다. 갑이 을을 축으로 삼아 병을 들어올렸어요. 병은 공중부양 되었습니다. 갑과 병이 공중에 떴으므로 모든 무게를 을이 감당합니다. 이게 이해가 안 된다구요? ### 진짜 이것을 이해 못하는 사람이 있기는 있군요. 조금 더 전개하면 우주 안에 이 그림과 다른 구조는 없습니다. 단 한 개도 없어요. 여기서 사람이 셋이고 막대가 하나인데, 구조론은 5이므로 한 명이 더 있어야 합니다. 무조건 5여야 하고 5가 아니면 아무 것도 할 수 없습니다. 물론 막대기로 대체할 수 있으므로 실제로 사람이 5명이어야 하는 것은 아닙니다. 돌이든 막대기든 포지션이 다섯 있어야 해요. 구조론을 학습했다면 이런건 그냥 보면 1초만에 보여야 합니다. 왜냐하면 우주 안에 구조는 이거 하나 뿐이고, 다른 구조는 절대로 없으니깐. 눈 씻고 봐도 없어요. 축과 대칭이라는 거죠. 콤파스이기도 하고. 예컨대 젓가락은 콤파스가 아니잖아요. 근데 젓가락을 손으로 쥐면? 콤파스죠. 사람이 가만이 서 있으면? 두 다리가 콤파스죠. 위 저울도 접시가 둘이니까 콤파스죠. 콤파스는 축과 대칭이고 우주 안에 다른건 없습니다. 우주 안에 인과법칙을 벗어날 수 있는게 없으므로 이건 절대진리입니다. 인과율도 가만이 생각해보면 그대로 콤파스임을 알 수 있습니다. 원인과 결과 두 포지션이 축에잡힌 것입니다. 모든 물건이 저울로, 콤파스로, 시소로. 축과 대칭으로, 소실점으로 보인다면, 모든 사물에서 1초 안에 콤파스를 찾아낼 수 있다면 그 사람은 구조론을 아는 사람입니다.
그래도 안 믿어진다는 분은 이걸 따라해 보세요. 안 됩니다. 자 세 손가락을 펴고 그 위에 볼펜을 올려놓아 보세요. 다음 한 손가락을 떼세요. 볼펜은 반드시 땅으로 떨어집니다. 즉 사진의 이 모양은 본드로 붙이기 전에는 안 되는 겁니다. 그럼 나는 어떻게 이걸 연출했느냐? 볼펜 뚜껑을 빼서 새끼손가락쪽을 가볍게 했죠. 즉 무게중심을 이동시켜 간신히 사진을 찍은 거고, 정확히 거리를 맞추면 볼펜은 반드시 손에서 굴러떨어집니다. 해보세요. 지금 볼펜은 왼쪽손가락이 들린 겁니다.
그래도 이해가 안 되는 분은 마지막 수단으로 책상 위에 이렇게 연필을 올려놓아 보세요. 딱 가운데 맞춰두면 연필은 백퍼센트 바닥으로 떨어집니다. 이 사진은 오른쪽에 많이 치우치게 두어서 아슬아슬하게 버티고 있는 거에요. 길이를 자로 재서 딱 가운데 위치시키면 반드시 떨어집니다. 왜냐하면 지우개 쪽이 더 무거우니깐. 이게 다 같은 구조라는게 보이지 않습니까? 구조론이 어렵다는 분은 이런 기초적인 훈련이 안 되어 있다고 봅니다. 지구 안의 모든 존재는 5포지션인데 그렇지 않은 것처럼 착각되는 이유는 중력이 눈에 안 보이기 때문입니다. 우주공간이라고 생각해 보세요. 여기서는 움직임 형태로 중력을 발생시킨 것이고. 즉 에너지를 작동시킨 거지요. 사회에서는 의사결정이고.
이렇게 됩니다. 뒤가 공중에 들려요.
결과는 추락. 이젠 진짜 이해가 되었을 겁니다. 앞사람이 공중에 뜨면 대칭원리에 따라 뒷사람도 공중에 떠서 추락 |

-
- 1.jpg [File Size:39.4KB/Download:8]
- 2.JPG [File Size:11.4KB/Download:6]
- 5.JPG [File Size:14.9KB/Download:5]
- 7.jpg [File Size:16.0KB/Download:5]
- 9.JPG [File Size:14.1KB/Download:5]
- 3.jpg [File Size:62.0KB/Download:5]
- 11.JPG [File Size:28.9KB/Download:5]
- 20140331_220140.jpg [File Size:152.0KB/Download:5]
- 20140331_221244.jpg [File Size:91.0KB/Download:5]
- 2014033.JPG [File Size:19.6KB/Download:5]
- 2.JPG [File Size:15.3KB/Download:5]


일단 감사드립니다.
전부터 볼펜이라던지 그 외 모든 것들이 구조로 이루어져 있다는 것은 알고 있었습니다.
다만 이 그림만큼은 이게 어째서 볼펜과 같은 구조인지를 모르겠다는게 제 문제입니다.
사람이 두발로 움직이는 것이나 그냥 서 있는 것이나, 볼펜을 쥐고 글자를 쓰는 것 등에서 제가 구조를 느끼는 것은 구조적으로 밸런스를 이루어 그 형상이나 상태가 유지되는 이를테면 정지 영상 상태가 가능하다는 것을 느꼈었습니다. 물론 실제로는 끊임없이 일하고 있는 것이겠지요.
그런데 이 그림에서는 저울이 좌에서 우로 움직이고 있기 때문에 구조라고 인식하지 못한 것입니다.
출석부에 써 놓으신 글을 보고 저 그림이 왜 불가능한지는 단번에 인식했습니다.
하지만 여전히 아랫 단락들은 이해가 되질 않습니다.
###
* 위에서 언급하신 내용입니다.
여기서 사람이 셋이고 막대가 하나인데, 구조론은 5이므로 한 명이 더 있어야 합니다. 무조건 5여야 하고 5가 아니
면 아무 것도 할 수 없습니다. 물론 막대기로 대체할 수 있으므로 실제로 사람이 5명이어야 하는 것은 아닙니다. 돌이든 막대기든 포지션이 다섯 있어야 해요.
* 이전에 설명하신 내용입니다.
그림은 논외로 하고 이론으로 봐야 합니다.
축과 대칭이 있는데 축 1 대칭 2로 포지션 3이 그냥 날아갑니다.
기본적으로 3자리 빼고 나머지 두 자리로 건너야 합니다.
나머지 둘 중에 하나가 허공에 뜨기 때문에 결국 한 사람만 건널 수 있습니다.
허공에 뜬 사람과 맞은 편으로 건너갈 사람을 합하여
두 사람의 체중을 보장해야 하므로 반대쪽에 3이 있어야 합니다. 합쳐서 5죠.
###
한명이 더 있으면 건널 수 있다는 것은 알겠는데 그것이 왜 구조론의 5와 연결되는지 이해가 되질 않습니다.
한명이 더 있는 것은 그림상에서 좌측으로 무게 중심 자체를 옮겨 놓은 것 또는 구조가 오른쪽에서 좌측으로 이동한 것으로 밖에 인식되질 않거든요.
구조론에서의 5의 의미는
외부의 정보를 내부로 끌어들여 다시 피드백하는 과정의 의사결정 단계 5로 알고 있는데
이 그림에서 그냥 숫자 5를 맞추는 것과 연결시키려하니 헷갈리기 시작합니다.
동렬님께서 친절하게 게시판에 써주신 것은 제가 어떻게 감사를 드려야 할지 모르겠습니다만,
이것을 이해 못하는 것은 제 문제라고 보입니다.
아마도 전 아직 구조론의 5를 정확히는 모르는 것으로 보입니다. 대충알고 있다는 뜻입니다.
질이 형성되는 과정과 그것이 구조를 통해 피드백 되는 과정, 완전성의 개념 등은 늘 그렇게 되는 것을 일상에서 보고 있으니 알기가 쉬웠습니다.
하지만 그것이 내부적으로 4의 각 포지션을 이루는 과정을 아직은 이해하지 못한 것으로 보입니다.
어차피 책에 다 써놓으신 것입니다. 좀 부끄럽네요. 좀 더 읽어보겠습니다.

늘 하는 다짐이지만 조금 더 기다려주세요.
시간이 필요한 것이지 불가능한 것은 아니니깐요.

 김동렬
김동렬
차우님은 구조론의 근본을 묻고 있는데
1초만에 이해할 수 있는 간단한 것이지만 텍스트로 쓰면 책 한 권이 됩니다.
일단 세상이 구조로 되어 있다는 대의를 이해하고 있나요?
구조가 에너지의 입출력을 의미한다는 사실을 알고 있나요?
인과율을 이해하고 있나요?
인과율을 이해하는 사람은 없습니다.
인과율이 틀렸기 때문이죠.
(뉴튼이 틀렸지만 틀린게 아니듯 인과율도 낮은 수준에서는 맞습니다.)
먼저 제가 말하는게 모두 사건기준, 상호작용 기준임을 알고 있나요?
사건에 5가 필요하다는 말입니다.
그냥 돌이 있는데
이게 중력을 처리하는 사건으로서의 돌이냐
그냥 돌이냐는 다른데 이 차이를 알고 있습니까?
그냥 돌은 돌인데 사건의 돌은 5입니다.
돌 안에 5가 있다는 거죠.
돌에 작용하면 반작용해야 하니까.
반작용하려면 내부에 콤파스를 만들어야 하니까.
안개나 팥죽이나 물이나 바람은 5가 아니라서 반작용을 못합니다.
5를 이루어야 반작용을 하고, 그래야 사건이 일어나며 그래야 존재가 성립입니다.
위에서 5이어야 하는 이유는 내부에 콤파스를 만들어야 하기 때문입니다.
무엇을 하려면, 그것은 에너지 처리이며, 콤파스가 에너지 처리기입니다.
에너지를 대칭>비대칭하려면 일단 대칭에 3이 필요하지요?
이거 납득했습니까? 대칭은 3이다. 납득했어요?
그럼 비대칭은 2다 합치면 5다 납득했습니까?
1회의 사건이 에너지를 처리한다는 개념을 납득했냐고요?
일단 대칭의 3이 필요하고, 다시 일을 할 1이 추가되며 거기에 입력 1을 투입하면
1이 나갑니다. 즉 콤파스에 1이 들어오면 1이 나간다는 거죠. 그것이 구조의 복제입니다.
붓으로 글씨를 쓴다면 일단 종이와 붓이 필요하겠죠.
그것을 총과 과녁이라 해도 좋고, 쟁기와 밭이라 해도 좋고, 자지와 보지라 해도 좋고.
하여간 어떤 둘이 있어야겠지요? 그렇죠?
권투라면 때리는 넘과 맞는 넘이 필요하겠죠?
이것도 납득이 안 된다면 패죽이고 싶음. 혼자서 권투 해 보라고.
밥을 먹는다면 사람과 밥 둘이 필요하죠? 그렇죠?
그렇다면 일단 2는 납득한거죠?
2를 어떻게 연결시킬까? 대칭으로 연결한다. 대칭에는 3이 필요하다. 합은 5다.
하여간 모든 구조는 대칭과 비대칭 곧
3으로 세팅하고 하나를 넣으면 하나가 나갑니다.
볼펜이든 돌이든 투수가 공을 던지든 총을 쏘든 활을 쏘든
모든 구조는 3에 1넣고 1나가는 구조입니다.
일일이 물어보고 확인을 거쳐야 하므로 하세월에.


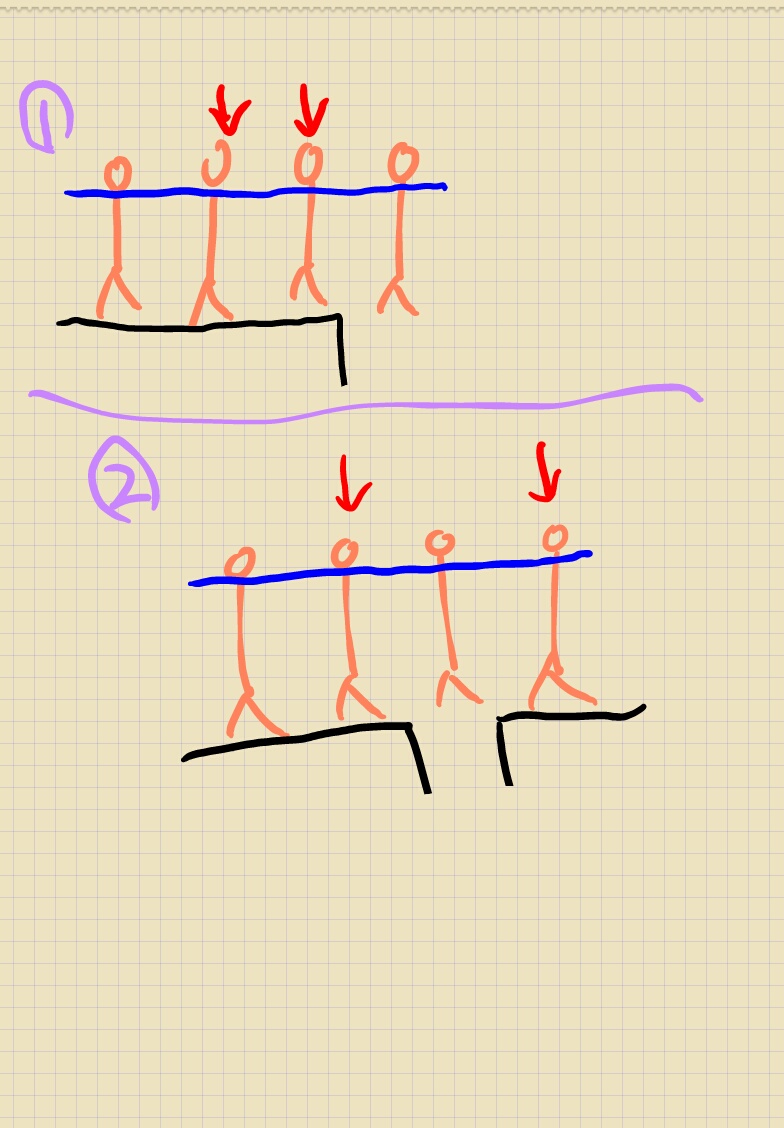
빨간 화살표가 힘을 받는 사람입니다.
1번의 그림도 결국은 버틸 수 있는 힘이 늘어난 것뿐이며 2번의 경우에도 마찬가지입니다.

 김동렬
김동렬
워낙 엉뚱해서 직접 대화해야 할듯

 김동렬
김동렬

문제는 구멍이거덩.
구멍이 없다면 그냥 가면 되야.
근데..건넌다고 생각하지 말고..
그 구멍을 수평으로 무한 확대해 보자구..
즉,
절벽으로 간주하고 한번 가보자구..
어떻게 될까..
어느 지점에서 봉이 꺽여 추락하냐?

 김동렬
김동렬
2) 여기서 무게를 논하는 것은 무의미하고 핵심은 착각입니다. 힘의 방향을 착각하고 있는 거에요. 착각이 없다면 구조론이 필요한게 아니죠. 깊이 살피지 않으면 대부분의 사람들이 모두 착각하는게 문제.
특별히 훈련되지 않으면 백퍼센트 착각한다는게 구조론이오. 그러므로 초등학교부터 구조론 훈련을 받아야 하오. 예컨대 바닷가에서 작은 보트를 타고 가다가 큰 배에 옮겨타라고 하면 처음 하는 사람은 백퍼센트 물에 빠집니다. 혹은 물에 빠질뻔 합니다. 큰 배에 옮겨타려고 배 난간을 붙잡는 순간 보트가 뒤로 가버리거든요. 그런 동영상 가끔 있죠. 의도와 반대로 되는 거죠.
4) 뭔 말씀인지, 엉뚱한 주장이오. 한 사람이 공중에 뜨는 순간 지구 중력이 입력되었지 않소? 무게가 나눠지고 합쳐지고 한게 아니고 저울에 무게가 처음으로 입력된 것이오. 한 사람이 공중에 뜨기 전에는 0킬로그램이었소. 저울에 올라가지 않은 체중은 논외. 통나무도 논외.

그러나 축이 통나무의 길이를 벗어날수는 없음
그렇게되면 사건이 불성립되므로
지구의 축도 지구를 벗어날수는 없음
축이 움직여 뭔가를 해결한다는 것은
그 범위가 있음
그 범위를 파악하는 것이 먼저임
축을 움직이면 어디서 부터 어디까지 영향을 미치는가...이것이 전체를 보는 것
이 축은 사건에서 고정되어 있다기보다 순간적으로 발생하는 경우가 많음
그러나 훈련되지 않아서 대체로 그것을 모름
순간적인 축의 발생은 지나가는 구경꾼도 축의 역할을 할때가 있음
축이 움직이지 않는 사회는 변화가 없는 사회...역할이 고정되어 있다고 믿는 한 축을 이해할수는 없는 것
저 세 사람이 통나무를 메고 모두 건너가려면
가운데 여자아이가 움직이는 수 밖에 없음
앞에 남자 아이가 건너려면 여자 아이가 뒤로 움직여
뒤의 남자 아이와 같이 버티는 힘으로 작용해야 하며(힘의 비대칭) 이때 앞의 남자 아이는 그 힘에 의해 건너감. 앞의 아이가 건너가서 양쪽에서 힘의 대칭을 이루면 가운데 있는 여자 아이가 이동...여자아이가 건너가면 다시 힘의 방향이 바뀜(힘의 비대칭)
축의 이동으로만 모두 건너갈 수 있음.
힘의 균일 상태 - 축이 뒤로 이동(힘의 비대칭이 한번 작동) - 대칭 - 축이 앞으로 이동(힘의 비대칭이 두 번 작동)

축 이동을 반대로 얘기하신 것 같네요.


축이 뒤로 이동하면 본문 그림에 지구를 지렛대로 들어 올리는 것처럼 뒤가 들리고 앞은
내려가는데 그러면 사람이 빠져서 못 건너가지 않나요?

축을 무엇이라 생각하시는 잘 모르겠네요.
그래서 다시 더 풀어서 설명합니다.
(저 사진에는 먼저 전제가 필요합니다. 통나무를 모두 어깨에서 내려 놓지 않은 상태에서 모두 건너가야 한다. 라 치고)
축이 뒤로 이동하면, 맨 뒤의 남자 아이가 통나무를 팔로 누르며 지탱하는 힘과 앞의 남자 아이가 매달리는 힘이 균형을 이루어 대칭을 이룹니다. 그렇게 앞의 남자 건너감(축의 이동으로 힘의 비대칭 형성되면
, 뒤의 남자 아이는 앞의 여자 아이 어깨를 지렛데 삼아 팔로 통나무를 누르며 버팀. 그러면 누르며 버티는 힘과 매달리는 힘이 시소의 균형 상태가 회복됨- 축이 뒤로 움직여 대칭 상태를 만듬) -> 앞쪽 남자 아이가 건너가면, 앞쪽 남자아이의 매달리는 힘은 누르며 버티는 힘으로 힘이 다시 전환됨, 뒷쪽 남자 아이도 앞쪽 남자 아이의 버티는 힘을 지렛데 삼아 누르는 힘 상태를 유지-축이 다시 중앙으로 이동된 상태, 시소가 균형을 이뤄 대칭된 상태. 중앙에 축이 있으면 시소의 양쪽이 균형 상태가 되어 대칭을 이루므로 이때의 축의 힘은 제로 ..상쇄됨...시소가 균형을 이뤘으므로 매달려 건너감( 이때는 축이 중앙으로 이동되어 시소의 완전 균형 상태, 완전 대칭 상태에서는 축의 힘이 제로가 됨....비대칭 상태가 아니기 때문, 축의 역할이 드러나지 않는 상태) -> 여자 아이가 건너가면 다시 축이 앞쪽으로 이동, 힘의 비대칭 상태로 시소의 균형을 다시 이룸, 뒤쪽 남자 아이 매달려 건너옴.
(축이 뒤로 이동하여 힘의 비대칭 형성- 시소의 균형을 만듬- 비대칭으로 대칭 형성, 축이 움직여 비대칭이 형성될때 축의 존재를 알게됨) -> (시소의 완전 균형 상태, 이때는 축이 중앙에 있어서 비대칭 상태가 아님, 축의 힘이 제로 상태 - 일반적으로 말하는 대칭 상태 - 대칭이 눈으로 보이나 축은 안보이는 상태) - > 다시 앞의 경우가 반복 - 앞의 경우가 축의 이동이로 앞쪽에서 나타남.
즉,
축 뒤로 이동 -비대칭 형성- 시소의 균형으로 대칭이 한 번,
축 중앙으로 이동 - 시소의 완전 균형 - 완전 대칭으로 대칭 두 번,
축 앞쪽으로 이동- 비대칭 형성 - 시소의 균형으로 대칭 세 번.
축의 이동으로
비대칭에 의한 대칭 - 완전대칭 - 비대칭에 의한 대칭
이렇게 총 세 번의 대칭이 만들어져야 건너갈 수 있음.

 김동렬
김동렬
아란도/ 이 문제는 상황이 통제되는가입니다.
상황을 통제하려면 콤파스를 만들어야 하므로 다섯 포지션이 필요하다는 거죠.
먼저 앞사람이 허공에 떴을 때 지구의 중력이 들어와서 포지션 하나를 가져갔어요.
그 이전에도 중력은 있었지만 발바닥을 통해 지구로 되돌아갔으므로 논외.
앞사람이 허공에 떠서 지구로 돌아가지 못하는 중력이 발생했으므로 에너지의 입력, 사건시작.
맨 앞이 질이므로 두번째가 입자, 입자가 가운데 센터가 되어 중량 전체를 부담하고
뒤에 오는 사람이 힘, 힘은 방향을 바꿉니다.
착각하는 분이 있는데 두번째 사람이 괴력의 소유자여서
열명을 한 팔로 들고 건널 수 있다고 해도 그게 구조론의 답은 아닙니다.
실제로 이걸 건너느냐의 문제는 아닙니다.
포지션이 갖추어졌느냐입니다.
포지션이 없으면 슈퍼맨도 건너지 못한다는 말이지요.
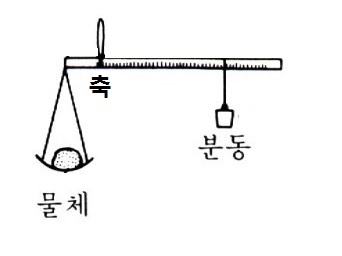
대저울은 첫째 계량할 물체.. 1번 사람.
둘째 저울을 걸어맬 축..2번 사람
세번째 분동,, 3번 사람
넷째 막대.. 통나무
다 있는데 하나가 빠졌습니다.
뭐가 빠졌나요?
아란도님은 축이 뒤로 가야한다고 말씀하셨는데 이 그림을 보세요.
축이 앞에 있습니다.
눈금이 빠졌잖아요.
눈금을 만들려면 충분한 길이가 필요합니다.
죽 축을 중심으로 왼쪽보다 오른쪽이 최소 두 배 길어야 하는 거지요.
물체와 분동의 무게가 같을 때 그렇고 보통 물체가 더 무거우므로 졸라리 길어야 해요.
근데 원래 그림은 통나무 뒷쪽이 충분히 길지 않아요.
두번째 사람이 앞으로 조금 이동하고 맨 뒷 사람이 통나무 끝에 매달리면 되지만
그건 이론적인 해결책이 아니라 꼼수이므로 논외.
한 명이 더 투입되거나 통나무 길이를 늘리거나 축을 앞으로 옮겨서
포지션을 추가하는게 정답입니다.
그래야 대칭이 작동해서 상황이 통제됩니다.
구조론으로는 입력 저장 제어 연산 출력인데
두번째 사람이 저장, 이때 전체를 저장합니다.
두번째 사람이 세 사람의 무게와 통나무 무게까지 몽땅 감당합니다.
그러므로 소실점이 되는 거죠.
이렇듯 한 점이 전체를 대표하는 소실점은 우주 안의 모든 사건에 있습니다.
누구든 당신도 우주의 대표자가 되어야 하는 지점이 있다는 겁니다.
두번째 사람이 슈퍼맨이면 건널 수 있지만 그것도 꼼수에요.
구조론으로는 어떤 경우에도 못 건넙니다.
그냥 통나무 길이를 늘리고 두 번째 사람이 약간 앞으로 이동하면 됩니다.
모든 상황의 통제는 대칭으로만 가능하다는 것이 이 물음의 본의입니다.
작용반작용을 성립시켜야 하니까요.

구조론으로 논하려면 실제로 그림을 그녀 보던지 머리속에서 시물레이션 해보던지 이겠지요.
시물레이션 해본 결과 통나무가 훨씬 더 길어야 하는 것은 맞고,
세 사람이어도 건널 수 있는 것도 맞고, 이미 통나무를 메고 있는 세 사람이 같은 상황에 있는 것도 맞고, 공동운명체라는 것도 맞고, 같은 계 안에 있는 것도 맞고, 셋의 힘이 균등하다라는 전제가 있어야 한다는 것도 맞고, 땅바닥에서 이미 중력이 작용하고 있는 것도 맞고, 그럼으로 이 모든 것이 질인 것이고, 입자는 통나무를 메고 있는 이들인 것이고, 이들이 다시 그 안에서 축을 움직인 운동과 힘을 이동하여 실제로 그들이 움직여 운동으로 건너가고 다시 양으로 해소 되는 것이겠지요.
그리고 세 사람이 건너가려는 방향과는 반대로 축이 먼저 뒤로 움직여야 반동으로 앞사람이 건너가게 됩니다. 뒤로 움직여서 일어난 힘의 변화는 윗글에서 설명했으니 생략합니다.
그리고 모두 대칭을 형성하게 됩니다. 이 대칭 형성들이 바로 작용반용인 것이니까요. 통나무가 무한정 길고 사람이 훨씬 더 많다 하더라도 적용되는 것은 같다고 봅니다.
이것을 다른 상황들에 적용한다 할지라도...
축이 움직여야 뭔가 새로운 힘(비대칭에 의해 다시 대칭이 만들어짐)이 나오고 또 완전한 대칭(축이 힘을 사용하지 않는 상태)을 이루려면 축이 움직이지 말아야 합니다. 이것은 상황에 맞춰져야 하는 것이므로 곧 판단인 것이니까요.









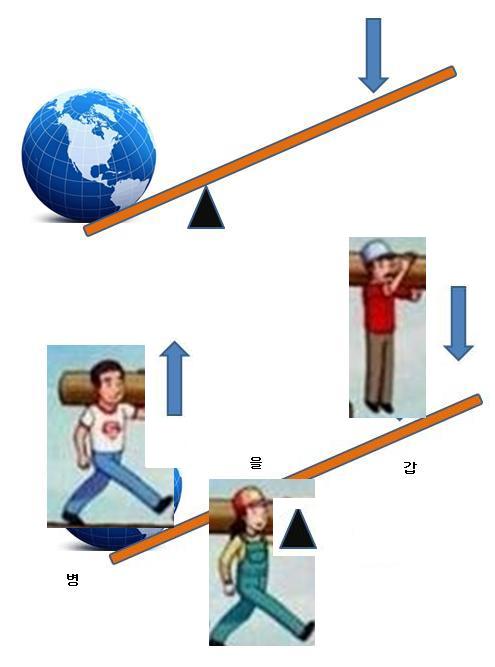










일반 사람은 자신 체중의 3배를 들지 못합니다.
88서울 올림픽 때 터키의 모 역도 선수는 체중의
3배를 들어 금메달을 땄는데 그 기록이 윗 체급
1위 기록 이상이었습니다.
역도도 중량급으로 갈수록 1위 기록이
자기 체중의 2배 이하로 줄어듭니다.
만약 사람이 아니라 자신 체중의 3배를 들 수 있는
로보트를 썼다면 첫 번째 그림의 일은
결코 불가능하지 않을 것입니다.