천만관객 시나리오가 이렇게 완성 되는건가요
세월호 수입할때 은행이 자본도 없는 놈들에게 대출해줘서 청해진 해운은 돈한푼 안들이고 세월호를 수입했다고 합니다. 이 돈을 은행에서 대출해줄때 그냥 해주지는 않았을 것같습니다. 뎃글에 보니 이명박이가 수입을 허락했고 돈은 국가에서 보증했을것이고 그래서 국정원이 관리했을 것이다. 라고 하네요. 사고책임은 선원들에게 있을지 몰라도. 세월호의 주인은 국정원이 맞는지도....


 담 |/_
2014.07.28.
담 |/_
2014.07.28.
"선두경쟁하는 팀이어서" ㅎㅎㅎ 흐믓한 대목.
"다 잘 할 필요 있나. 잘 되는 것 잘 사용하면 되지." 역시 되는 돼지 ㅋㅋㅋ.

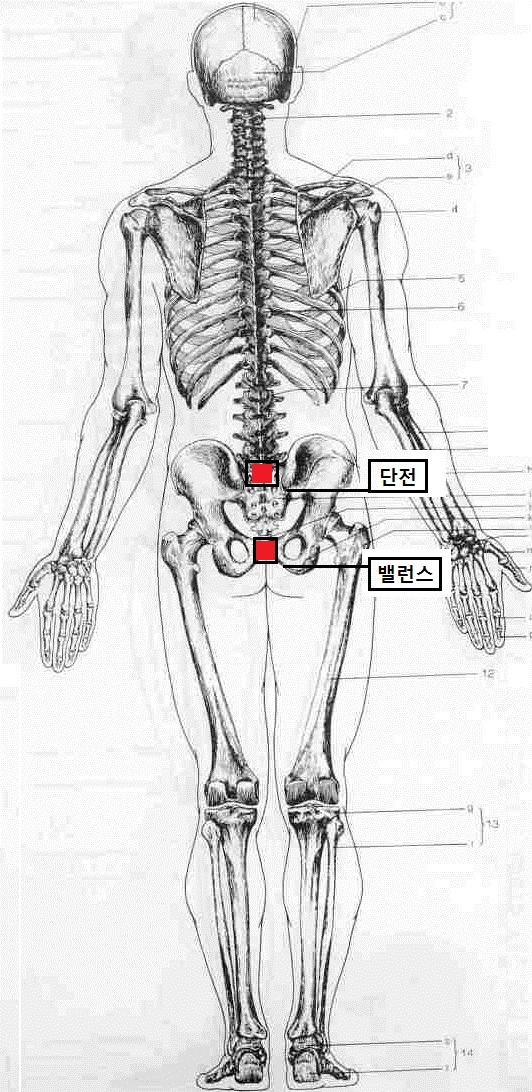
저기를 중심으로 옆으로 줄을 그으면
대퇴와 골반이 연결되는데 코어라고 합니다.
몸의 가장 중심인 거죠.
코어를 강화시키는 운동이 스쿼트나 데드리프트.

"똥구멍에 힘주고, 힘차게 걸어가는 거여.”
나와 선인님은 한목소리로 늘 읊는 대사를 말했다.

서양인 비례: 몸통과 머리를 합한 것(상체)이 하체(다리)길이와 같고
동양인 구조: 다리가 몸통길이와 같고, 상체기준으로보면 머리만큼 짧다.
대체로 체형이 위와 같은 것 같은데, 다리의 길이가 머리하나의 차이가 있다면
중심도 바뀌어야 하지 않나 싶네요^ 즉, 서양인은 x꼬, 동양인은 단전...?
(위성미 사진은 서양인 비례로 예외)

 김동렬
2014.07.28.
김동렬
2014.07.28.
단전은 어떤 얼빠진 머저리가 지어낸 엉터리 개념입니다.
그딴건 해부학적으로 존재하지 않습니다.
인체구조 상 다리뼈 위에 척추뼈가 얹혀있죠.
둘이 만나는 뾰족한 지점이 있는데
팽이가 뾰족한 촉 부분이 땅 위에서 도는 것과 같이
포크트릭의 한 점이 얹히는 것과 같이

밸런스의 소실점역할을 하는 한 점이 있는 거지요.
그게 단지 길이의 중간은 아닙니다.
그런데 길이의 중간일수록 밸런스잡기가 쉽습니다.
상체가 너무 길거나 혹은 하체가 너무 길어서 밸런스가 어긋나면
근육을 보강해서 체중으로라도 밸런스를 맞추면 됩니다.
혹은 폼을 교정해서 밸런스를 잡아도 됩니다.
포크트릭처럼 균형이 딱 맞으면
한 점을 제어하여 계 전체를 통제할 수 있는데 그게 밸런스라는 거죠.

살을 발라내고 뼈만 보니 어디가 만나는 지점-중심인지 알겠네요.
생식기가 있는 곳이 중심이네요.가장 중요한 역할을 하는 곳이니.생장점.

그리고 털이 많은 곳이 머리털 빼고는 생식기와 겨드랑이 인데 다 몸통과 만나는 곳.
교통로에 숲이 있군요.

 김동렬
2014.07.28.
김동렬
2014.07.28.
겨드랑이와 생식기는 냄새를 피우려는 것(페로몬.. 편안하게 함)
머리카락은 자신을 감추려는 것.(생존전략, 보호색)
수염과 대머리는 자신을 과시하려는 것(수컷의 갈기나 수컷 새의 화려한 깃)

태극권 선생님이 단전은 단전에 있지 않고 회음에 있다고 늘 강조했었던것이 이 원리때문이었던듯.

 김동렬
2014.07.28.
김동렬
2014.07.28.
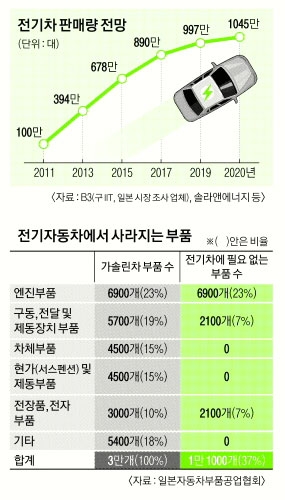
유치한 음모론에 불과합니다.
GM이 그 기술 있었다면 세계시장을 다 먹었고
미국은 살판났고 CIA가 전면에 나섰겠죠.
미국놈들이 어떤 놈들인데?
당시만 해도 일본차에 개처럼 얻어맞던 시절이라
미국자동차산업이 통째로 붕괴될 판인데.
미국이 일본차를 견제하기 의한 꼼수 회피기동의 일환으로
각 기업에 무공해차 생산을 강제했는데
EV1은 정부의 압박에 따른 보여주기 생산이라
돈 들어가는 보여주기가 끝나고 생산을 그만둔거죠.
EV1의 진짜 의미는 테슬라를 보면 알 수 있습니다.
전기차가 서민의 도심용 대안카가 아니라 슈퍼카로 진화될 가능성.

4학년에 나오는 평면도형이네요.
삼각형의 특징은 세변으로 이루어져있고, 세개의 꼭짓점, 세각의 합은 180도 이다 정도로
교과서에서 다룰 겁니다. 동렬님 말씀대로 평면도형은 만질 수도 없고, 추상화된 개념이기 때문에
현실계에는 존재할 수 없는 도형이지요.
다만, 도입할 때 어쩔 수 없이 구체물인 삼각형이나 삼각형 모양과 비슷한 교통표지판을 도입하지요.
물론 삼각자나 교통표지판도 얇아도 높이(두께)가 존재하므로 입체물이지만, 아이들의 이해를 돕기 위해서
어쩔 수 없이 도입하는 물건들이고...
정답이 분명 있는데, 정답은 얘기 안하고 다양성이니 창의성 운운하면 해당 학문이 산으로 가고
닫힌계가 무너집니다. 초등학교에서는 현실에서 다루기 쉬운 입체모양(입체도형으로 바로 개념화하면
어려우니까 생활속에서 볼 수 있는 구체물을 사용)을 저학년 때 다루고, 중학년때 평면도형,
고학년때 입체물을 개념화한 직육면체나 각기둥, 구 에 대해서 배우지요.
저 학생은 공부를 해본 적이 없고, 교과서 내용과 시험을 연결짓지 못했습니다.
저런 학생의 특징은 아주 기발한 창의성을 가진 아이거나, 아니면
공부한 게 생각이 안나니까 자기 경험대로 생각대로 그냥 쓰는 거지요.
목적어(대상) 개념을 염두하고사슴이 '거울을' 봅니다, 대신에 사슴이 미쳤나봅니다 라고 쓰는 것 처럼요.

 김동렬
2014.07.27.
김동렬
2014.07.27.
자연에는
점, 선, 삼각형, 사각형, 원
이 다섯가지 밖에 없습니다.
점은 가지끝처럼 끝나는 부분에 있고
선은 나뭇가지처럼 자라는 부분에 있습니다.
삼각형은 깨진돌에서 발견할 수 있고
사각형은 어떤 둘이 교차하는 곳에 있습니다.
구는 나무의 단면이나 어떤 점점 자라서 커지는 것에 있습니다.
도형을 그냥 도형이라고 하는건 잘못된 교육입니다.
그냥 있는게 어딨어?
그냥 그런건 있을 수 없지요.
물방울과 같은 구는 동적균형에만 있고
입체는 대칭구조에만 있습니다.
창의력은 이런 근본을 찾으려는 끝없는 노력의 결과물입니다.
그냥 제멋대로 생각하는건 그냥 얼간이죠.
과일은 왜 공모양이 되는지
집은 왜 사각형으로 짓는지
갈림길은 왜 삼각형이 되는지 생각해봐야 합니다.
거기서 직관력이 얻어지는 거죠.

시험지에 저렇게 쓴 학생이나 저나 그다지 차이가 없다는 것을 깨닫게 되네요. 추상화된 개념에 빠져 자연계에 이미 존재하고 있는 것을 없다고 했었음을 인정할 수 밖에 없네요. 특히 동적균형과 원, 대칭구조와 입체물에 대한 말씀과창의력이 어디서 나오는지에 대한 부분은 2학기때 아이들과도 함께 나눠야겠네요!

















게다가 확신범.