파동과 입자, 하나로 딱 떨어지지 않는 거시기한 그 놈
인류사의 큰 발전이 수학에 의한 것임에도 불구하고 인간이 가장 어려워하는 것이 있으니 바로 원자적 사고방식을 깨는 것이다. 반면 구조론의 핵심은 어떤 것이 있으면 반드시 그것을 구성하는 틀, 즉 전제가 있다는 것이다. 이것만 알아도 세상이 달라 보인다. 누구나 봤지만 말하지 못하는 것을 말하면 그게 깨달음이다. 말할 수 없는 이유는 당신 머리속의 언어의 틀 때문이다.
학교에서 배운 수학의 핵심은 딱 맞아떨어짐이다. 방정식이 대표적이다. 미지수가 있으면 그것을 간접적으로 표현하는 다른 구성소를 통해 우리는 그것을 추론할 수 있다. 기하도 마찬가지. 삼각형의 내각합이 180도라는 전제를 통해 두 각을 알면 나머지 하나를 추론할 수 있다. 수학이 빛나는 부분이다. 아마도 인류가 방정식을 표현할 수 있게 되었을 때 무척 뿌듯해 했을 것이다. 내가 아는 것을 너에게 전할 수 있고, 너는 남에게 전할 수 있게 되었다.
그런데 말할 수 없는 이상한 놈들이 나타나기 시작했다. 바로 무리수다. 딱 떨어지지 않는다. 이건 말이 안 되는 것이다. 똑 떨어지라고 수학을 만들었는데, 그 근본을 흔드는 것이다. 이쯤 되면 피타고라스가 칼부림을 해도 이상하지 않다. 제논이 역설로 인류를 비웃던 바로 그 지점. 인간은 이 말할 수 없는 비밀 앞에서 언제나 비겁하고 무기력했다. 우리는 구조론을 배운 자들이다. 인간이 말할 수 없는 것이 어떤 것인지 잘 알고, 그것을 말할 수 있는 방법도 안다.
수학의 딜레마는 언제나 원인이 하나인데 결과가 둘 이상인 놈이다. 비슷한 게 확률이다. 원인이 하나인데 왜 결과가 여러놈이야. 주사위는 하나인데 왜 눈이 6개지? 세상은 기계적인 것이 아닌가? 함수는 일대일 대응이 아닌가? 당신이 가진 컴퓨터에 a를 눌러보자. 그러면 a가 화면에 뜰 것이다. 근데 가끔 b도 뜬다면? 바로 빌게이츠한테 쌍욕을 박아야 한다. 그런데 말이다. 세상은 원래 의도가 확률로 나타난다.
프로그래머가 아무리 잘 만들어도 어딘가에선 그가 의도하지 않은 버그가 생기게 되어 있다. 늘 부작용sideeffect가 있게 되어 있다. 부작용 안 생기게 한다고 함수형프로그래밍을 만들어봤자다. 부작용이 덜 한 거지, 아예 없어지지는 않는다. 인류의 당황도 바로 여기에서 기인한다. 여친한테 꽃을 주면 웃어야 한다. 그런데 왜 안 웃지? 피타고라스는 마누라한테 꽃을 줬다가 싸대기를 맞았다. 그게 무리수고, 확률이고, 미적분이고, 허수이며 차원이다.
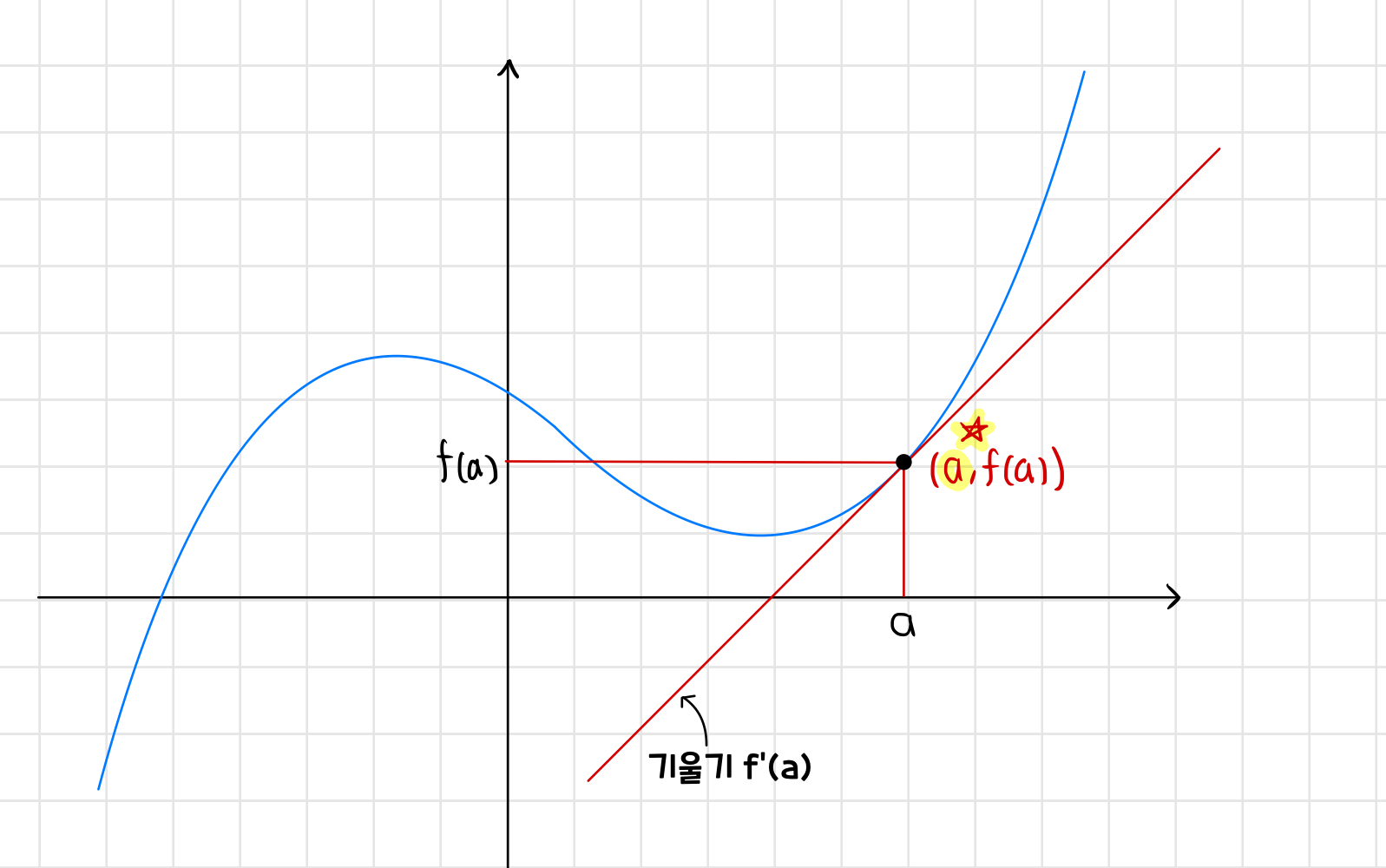
서두에 순간변화율(=접선의 기울기)을 꺼낸 것은 인간의 언어가 참 얄팍하기 때문이다. 그냥 하나(원인)에 둘(결과)이 묶인 ㅅ(혹은 Y)을 보여주면 되는데, 굳이 하나는 하나인 걸로 그걸 표현하려고 한다. 이게 얼마나 이상했는지 아예 학문을 만들었다. 코시의 입실론 델타 논법. 그리고 해석학. 괜히 해석(解析)이 아니다. 양파 껍질 벗기자고 만든 게 미분이다. 하지만 그들은 세상이 트리로 돌아간다는 것을 알면서도 수학의 선배들이 만들어 놓은 확고한 세계관을 등에 업고 눈앞의 사실을 왜곡한다.
순간변화율이라는 게 어떤 한 지점에 둘이 엮인 것이다. 무한히 다가간다는 극한이 사실은 2를 말하는 것이고, 극한점은 1이다. 곡선(2)이면서 동시에 직선(1)인 바로 그 지점이 똥꼬쇼가 펼쳐지는 곳이다. 엉덩이로 갈라지지만 똥꼬는 하나뿐이다. 무리수는 2로 이루어진 하나의 수다. 그래서 무한이 존재한다. 무한해서 무한이 아니라, 전제가 둘이라 무한이 생긴 것이다. 재귀함수 말이다.
우리가 절대적이라고 생각했던 어떤 한 지점이 사실은 2로 이뤄져 있었다는 것을 깨닫게 한 것이 무리수이다. 언제나 곱셈이 문제다. 곱셈과 나눗셈이 나오면 인간은 차원이라는 신을 만난다. 그렇다. 차원을 표현하는 것이 인류의 오랜 과제인 것이다. 무리수에서 한 번, 확률에서 한 번, 미적분에서 그리고 파동(2)과 입자(1)에서 인간은 그 유령을 또 만났다. 인간들이여, 그거 어렵지 않다. 그냥 트리다.
순간인데 변화가 가당찮다. 이게 뭔 개소린가 싶다. 그런데 그게 맞다. 나뭇가지는 하나에 둘이 붙었기 때문이다. 순간(1)에 변화(2)가 붙어있다. 그것이 순간변화율이며 파동과 입자의 이중성이며 불확정성원리이며, 불완전성정리이다. 음수나 양수나 제곱하면 모두 양수가 나온다. 이거 이래도 되나? 그게 기하학이다. 대수로는 설명이 불가. 길을 가르쳐줄 때, 그림을 보여주면 쉽지만 말로 하면 한참 헤맨다. 기하와 대수의 차이 때문이다. 누군가 당신에게 미적분을 설명한다면 속으로 웃어도 된다. 어차피 암 것도 모르는 거니깐.
순간을 벗기고 변화를 추출한다. 껍질 하나를 벗기고 나머지를 비교한다.비교하면 비율이고 기울기다. 그것이 도導함수요, 미분의 정의다. 순간이라는 공통 변수를 제거하여 변화를 측정하는 것이 미분이다. 현상을 측정했을 때, 이왕이면 시간이라는 가상의 변수를 제거하면 속도(m/s)요, 시간을 두 번 제거하면 가속도(m/s^2)다. 제논은 아킬레스와 거북이에 대한 공통의 제3변수를 말하지 않고 대신 서로를 서로로 재귀적으로 무한 비교하여 관측자를 스택오버플로우에 빠지게 하였다.
이는 피타고라스가 의심한 것이고 갈릴레이가 째려본 것이며 뉴턴이 확인한 것이다. 해밀턴이 확장하고 아인슈타인이 우주에 적용한다. 다시 확률로 정규분포로 나아간다. 그리고 모든 것은 양자역학으로 합쳐진다. 요사이는 과학자들이 편미분과 통계로 인공지능을 만들어보겠다고 난리다. 이것이 수학과 과학의 역사다. 별거없다. 그들은 자신의 위치에서 말할 수 없는 것을 말하려 각자 노력해왔다. 인간은 여기까지 왔다. 아킬레스와 거북이를 보았는가? 이제 미분으로 둘을 비교하라.









 김동렬
김동렬




수학은 골 때리는 것이고
이런 것을 시각화 해서 보여주면 사람들이 쉽게 알아먹을텐데
왜 시각화를 하지 않는지 그게 수수께끼.
유리수라는 것은 비례로 나타낼 수 있는 것.
깔때기에 1을 박아놓고 어떤 숫자를 좁은 쪽으로 밀어붙이면 반드시 닿는 지점이 있는게 유리수
왼쪽이 분자가 되고 오른쪽이 분모가 되어 분수로 나타내는 것.
깔대기의 각도를 분수의 분자라 치고 분모를 오른쪽에서 밀어붙이면
대부분은 천장에 박혀서 더 나아가지 못해
문제는 파이를 박았을 때 조금 틈이 생긴다는 것.
엥? 틈이 막힐때까지 조낸 때려박으면 되잖아?
틈이 생기는 이유는 선의 굵기 때문. 선을 무한히 가늘게 하면 되잖아..그게 파이값.
이런걸 시각적으로 설명하면 이해할텐데 수학자들은 그냥 말로 때우는거.