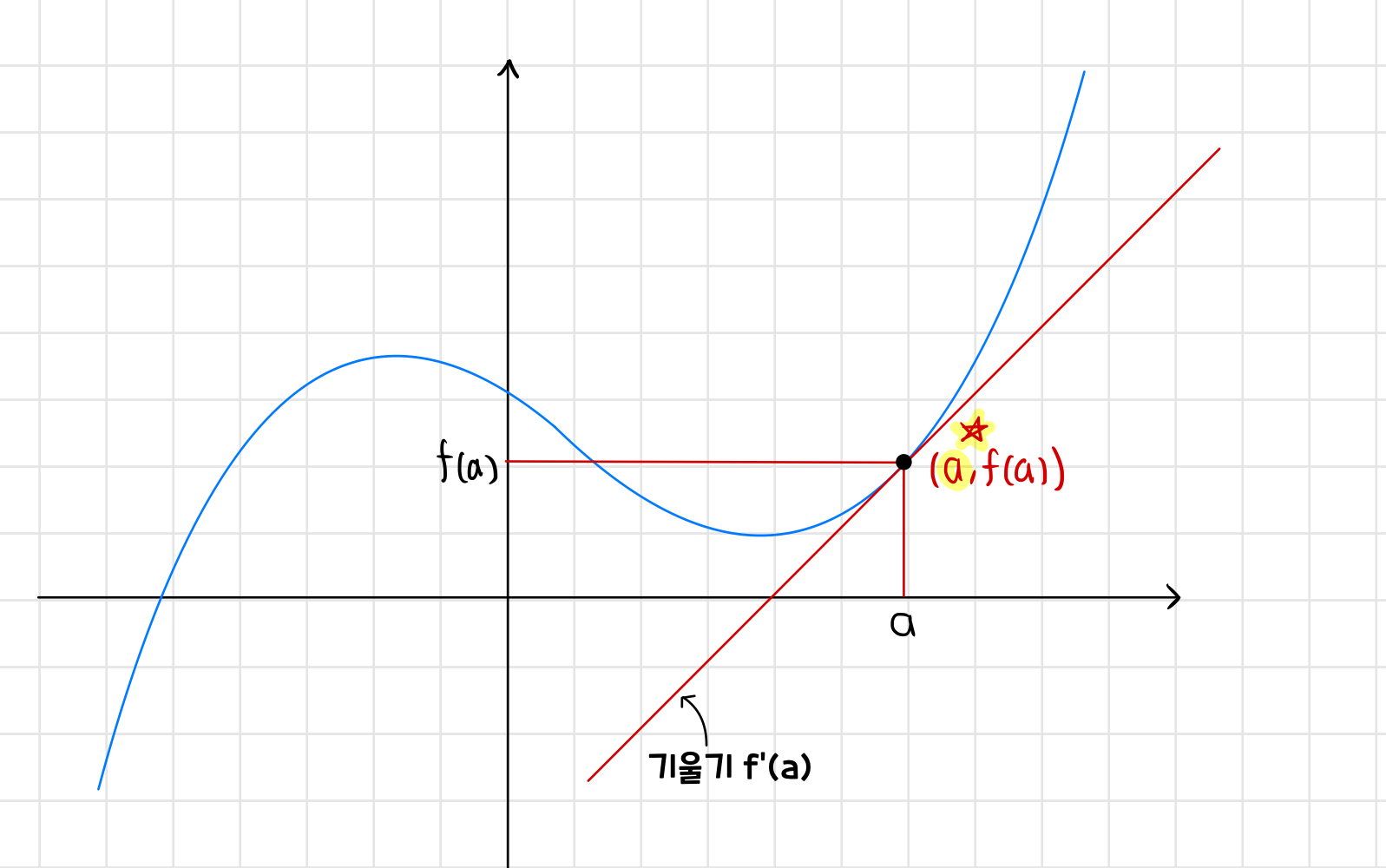
미분의 정의는 "어느 한 점 위에서의 접선의 기울기"라 할 수 있겠다.
상식적인 사람이라면 여기서 위화감을 느껴야 한다.
기울기는 반드시 2점 이상에서만 성립할 수 있기 때문.
도대체 한 점이라는 거야 두 점이라는 거야?
생각해보자. 점 하나를 통과하는 선의 개수는 무한대.
무한대 개수의 선을 줄이려면 둘 중 하나의 방법을 써야 하는데
다른데 점을 하나 더 찍어서 두 점을 통과하는 하나의 선을 도출하던지
아니면 2차 이상의 곡선 위에 접선이라는 개념을 사용하여 하나의 선을 도출하던지
대충 봐도 두 점을 찍는 문제는 아니므로
미분을 구하는 상황은 직선과 곡선이 중첩된 상황 그 자체를 의미하는 것이 된다.
즉, 접선 자체가 중첩 상황을 표현하는 것.
수학자들은 2천년 동안 이걸 말하지 못해서
리미트 어쩌구 저쩌구 하는건데, 내가 가슴이 답답해진다.
그렇다면 미분 상황에서의 일점은 일점이 아닐 수도 있다.
내가 보기엔 2점이지만 다른 사람이 보기엔 1점인 상황
위에서 보면 파동이지만 아래에서 보면 입자인 상황
파동을 미분하면 입자가 나온다는 말씀.
갈림길은 2갈래와 1갈래가 만난 길이다.
2갈래 입장에서 반대를 보면 1갈래이고
1갈래 입장에서 반대를 보면 2갈래이다.
이걸 누구 입장에서 불러야 하나? 헷갈리지롱.
그래서 에라 모르겠다, 그냥 갈림길.
이걸 답할 수 없다면 수학을 논하지 말라.
곡선의 의미는 2개 이상의 함수가 중첩된 것에 있다.
아인슈타인이 중력을 설명하며 곡면을 말한 게 다 이유가 있는 것.
"관측되는 현실 위에 그것을 낳는 뭔가 하나 더 있고, 그걸 미분하면
결과적으로 우리가 보는 현실이 있습니다."