http://math4ucanada.com/%EB%B2%A0%EC%9D%B4%EC%A6%88-%EC%A0%95%EB%A6%AC/
방증과 반증의 논리, 베이즈추론과 머신러닝
현대 머신러닝의 근간이 되는 논리는 베이즈추론법이다. 21세기의 엘리트라면 베이즈추론이 뭔지 정도는 알아야 하지 않겠나. 그런데 기실 베이즈추론은 사실에 대한 맥락적 해석법에 대한 것이다. 맥락이라고 하면 구조론과 닿는 점이 있다.
우리는 인셉션과 같은 영화의 결말을 열린결말이라고 한다. 그런데 사실 인셉션의 결말을 하나뿐이다. 그럼에도 불구하고 왜 우리는 이를 두고 열린 결말이라고 하는 것일까? 사실 열린 결말이라는 표현은 어색한 것이다. 열린 전제라는 표현이 더 정확하다.
우리가 결과를 해석함에 있어 그 의미를 다양하게 둘 수 있는 것은 사실 전제를 여러 가지로 둘 수 있기 때문이다. 우리는 어떤 사실이 그 자체로 고유하다고 생각하지만, 모든 사실은 전제와 진술의 형식으로 이루어져 있다. 즉 전제가 다르면 결과가 같아 보이더라도 그 결과에 대한 의미는 완전히 달라진다.
당신에게 베이즈확률이 어렵게 느껴진다면, 그것은 당신이 확률을 전제-진술 쌍으로 생각하지 않고 단순히 진술만으로 생각하기 때문이다. 결국 확률도 전제-진술 쌍으로 이루어질 수 있다. 아니 오히려 전제-진술 쌍으로 이루어져야 확률을 바르게 표현할 수 있다.
가령 기침을 한다고 해서 감기에 걸렸다고 할 수 있는가? 꼭 그렇지는 않다. 왜냐하면 미세먼지(반증)에도 기침을 할 수 있기 때문이다. 하지만 기침을 했다면 미세먼지를 마셨을 때보단 감기에 걸렸을 확률이 높을 것 같다. 이런 사고과정은 누구나 경험으로 납득하는 것이지만, 그 논리를 말하기는 쉽지 않다.
1) 감기O > 기침
2) 감기X > 기침
우리는 그냥 사실이 있다고 생각하지만, 모든 사실은 맥락적이다. 기침을 하더라도 다양한 원인에 의할 수 있다 그 원인을 추론하려고 하는게 베이즈추론이다. 즉 단순 사실이 아니라 전제-진술로 사실을 판단하는 과정을 확률적으로 논리화/수식화한 것이다. 베이즈추론은 기침과 같은 증거를 획득하고 이를 확률에 반영하여, 사전가정을 사후가정으로 갱신한다. 기침의 원인이 감기인지 다른 것(ex 미세먼지)인지를 판단하려는 것이다.
사전확률 + 증거(시행확률) > 사후확률(갱신확률)
길에서 무작위로 어떤 사람을 붙잡았을 때 그 사람이 감기에 걸렸을 확률은 얼마일까? 이때는 전인구집단에서 감기발병비율을 활용할 수 있다. 4월 한국에서 발병비율은 20%라고 한다면, 이는 길거리에 있는 사람을 무작위로 골랐을 때 그 사람이 감기에 걸릴 확률도 20%라고 생각하는 것이다.(사전확률)
그런데 그 사람이 갑자기 기침을 한다면? 기침은 감기에 걸렸을 확률을 강화시키는 하나의 증거가 된다. 물론 감기에 걸리지 않은 사람도 기침은 한다. 하지만 그 비율은 낮을 것이다. 보통 감기에 걸린 사람이 기침을 할 확률이 90%이고 걸리지 않은 사람이 알 수 없는 원인에 의해 기침할 확률이 30%라고 하자.(시행확률)
그러면 우리가 발견한 사람이 기침을 했을 때 그가 감기에 걸렸을 확률은 얼마나 될까? 즉 20%의 확률을 몇 퍼센트로 갱신해야 할까?(사후확률)
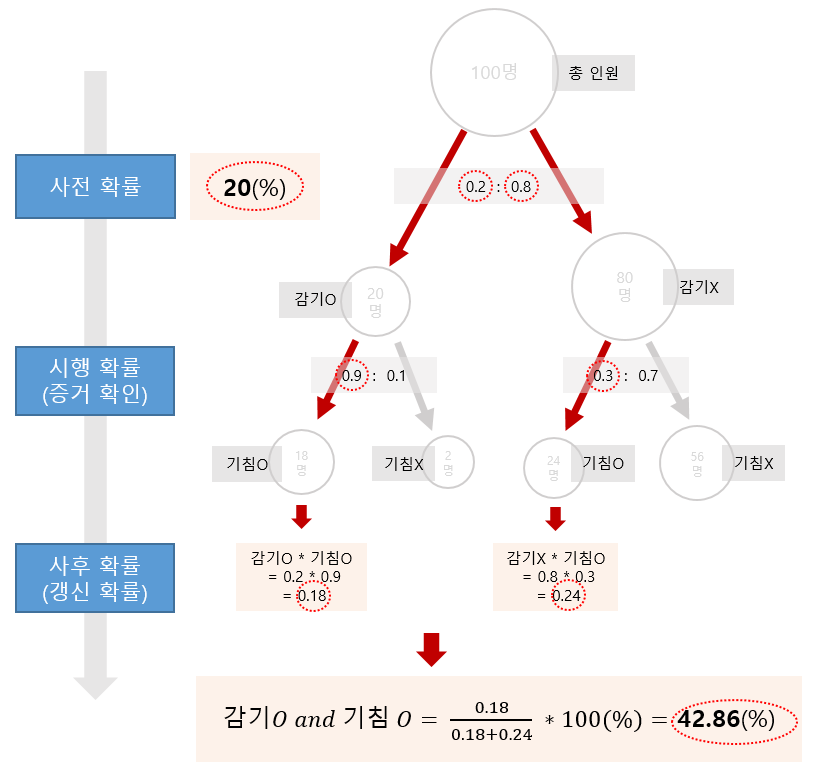
(모집단의 크기를 100으로 정한 후에 각 경우의 수를 이에 맞추어 양적으로 정규화normalize 하면 그림에서 원 안의 사람 수가 된다)
우리는 두 가정을 비교하려는 것이다. 즉 '감기>기침'인지 '미세먼지>기침'의 최종 비율을 계산하여 둘 중 어느 것의 확률이 더 높은지를 보려고 한다.
여기에 있는 곱셈은 각 단계의 확률 중 '실현된 확률'만을 각 단계에 '가중치'로 산입하여 큰 두 줄기의 최종값을 구하고자 사용된 것이다. 좀 더 쉽게 이해하려면 각 단계의 확률을 가중치라고 생각해야 한다.
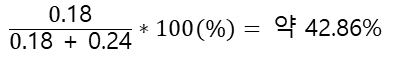
이 과정은 다음의 베이즈정리와 정확히 같다.
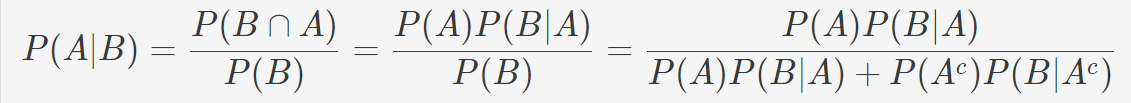
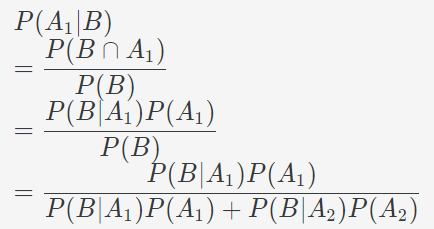
근데 왜 방증의 논리라고 할까? 증거 부분에 다양한 증거를 추가하면 사전확률을 더 갱신할 수 있기 때문이다. 감기의 경우라면 발열, 오한, 콧물 등이 추가 증거가 될 수 있으며, 이는 환자가 감기에 걸렸는 지를 확신할 수 있는 방증으로 사용될 수 있는 것이다. 다만 위의 그림은 단순하게 설명하고자 증거를 기침으로만 제시한 것이다.
내가 베이즈추론을 맥락적 해석법이라 말하는 이유는 일반적인 확률이 수평적인 비교, 가령 "감기o : 감기x = 10 : 90"과 같은 단선적인 것임에 비해 베이즈추론은 "감기0-기침 : 감기x-기침 = 10 : 90"과 같은 것이기 때문이다. 즉 비교 대상의 원소를 일자가 아니라 쌍자로 두는 것이다.
이는 구조론에서 사건의 기본 요소를 쌍자로 두는 것과 같은 맥락이다.














마지막 단락
*** 내가 베이즈추론을 맥락적 해석법이라 말하는 이유는 일반적인 확률이 수평적인 비교, 가령 "감기o : 감기x = 10 : 90"과 같은 단선적인 것임에 비해 베이즈추론은 "감기0-기침 : 감기x-기침 = 10 : 90"과 같은 것이기 때문이다. 즉 비교 대상의 원소를 일자가 아니라 쌍자로 두는 것이다.
이는 구조론에서 사건의 기본 요소를 쌍자로 두는 것과 같은 맥락이다. ***
에 대하여 부연, 질문을 드립니다. 구조론에서는 자연과 관측자와의 양자적 만남의 층위에 따라 관측값이 달라진다고 하고 있지요(읽는 분들께, 틀렸다면 지적 부탁합니다).
*** http://gujoron.com/xe/gangron/1197980
문제는 순간적인 성립이다. 반드시 5로 존재하지만 그중의 일부가 외부에서 순간적으로 조달될 수 있다. 충돌할 때다. 둘이 충돌할 때 이쪽의 3과 저쪽의 2가 순간적으로 5를 이루어 새로운 존재를 탄생시킨다. 이때 4 대 1이나 3 대 2의 결합이 있다. 그런데 인간의 관측 역시 그러한 결합을 한다는 점이 중요하다.
0에 서서 5를 보면 에너지가 되고, 1에 서서 4를 보면 물질, 2에 서서 3을 보면 공간의 3차원, 공간의 3에 서서 에너지의 입출력 2를 보면 시간이고, 물질 4에 서서 변화 1을 보면 정보다. 에너지, 물질, 공간, 시간, 정보는 인간이 단위 사건에 어느 정도로 개입하는지가 결정한다. 자신의 개입사실을 망각하는게 문제다.***
구조론의 말을 빌리자면 위 문구를 떠올릴 수 있겠습니다.
그렇다면 사전확률과 시행확률이라는 곧, '감기 유무-기침 유무'라는 양자적인 조건(혹은 만남)을 하나의 전제로 보아야 한다는 것으로 해석가능할지요?
즉 과거로부터 이제껏 누적된 데이터를 바탕으로 세운 전제(사람들이 100명 중 감기에 걸려왔던 데이터)인 사전확률이라는 조건과,
역시나 이제껏 누적된 데이터를 바탕으로 세운 전제(위에선 기침이겠지만 정확히는 '검사' 혹은 '단서'가 누적적으로 보여왔던 데이터. 이금재 님께서 글 초반에 걸어둔 링크에 의하면 유방암 검사의 정확도가 되겠군요)라는 조건을
수평적이며 양자적으로 동시에 생각할 수 있겠습니다. 이금재님께서 작성한 글의 도식에서 사전확률 다음에 시행확률로 화살표를 그려 순서를 나눠진 것은, 자연(사전확률)과 인간의 관측(시행확률)의 관계를 나타낸다는 점에서 구조론과 닿는 점이 있다고 할 수 있을런지요?
결국 '사전확률+시행확률' 혹은 '자연과 관측자'와 같이 양자적으로 성립하는 전제로부터 사후확률이라는 하나의 진술이 나온다고 할 수 있겠네요. 처음 글을 읽었을 땐 막연히 '전제-진술'을 양자적으로 말씀하시는 줄 알았지만 역시나 글을 끝까지 읽고나서 몇 번 더 읽어보니 글의 맥락이 조금 달리 보였습니다.
구조론에서는 질대칭 혹은 입자대칭과 같은 양자적 전제에서부터 질대칭(전제)의 진술인 입자(진술)로, 입자대칭(전제)의 진술인 힘(진술)로 사건이 방향성을 타며 진행하듯이, 상부구조의 수평적 만남(대칭)으로부터 하부구조로의 수직적(비대칭) 진행이 낳아진다고 하죠(읽는 분들께, 틀렸다면 지적 부탁합니다).
위 표현엔 혼동의 여지가 있을 수 있겠네요. 사실 '상부'구조 대칭으로부터 '하부'구조 대칭으로의 진행을 비대칭이라 표현한 것입니다. 사건 한 사이클로 크게 보자면 당연히 사건은 전체'비대칭'의 촉발로부터 부분'일시적인 대칭'으로 진행한다는 점은 숙지하고 있습니다.
글이 어수선해져서 이만 정리하자면 동어반복이긴 한데 제가 하려는 말은 '자연-관측자'라는 대칭으로부터 진행되는 사건의 경로는 필연적으로 하부구조를 향하듯이, '사전확률+시행확률'라는 대칭으로부터 사후확률(갱신확률)은 필연적으로(비대칭적으로) 낳아진다고(결정된다고) 볼 수 있겠다는 것입니다.
예컨대 관측값이 단순 '기침' 뿐이냐 혹은 '기침에 오한에 발열'이냐 또는 '기침에 누런 하늘'이냐에 따라 자연과 맞물린 정도가 다른 것이고, 그러므로 사후확률 역시 달라질 것이며, 역으로 '관측자+자연'이라는 조건이 감기이거나 미세먼지일 확률이 달라지겠지요.