입자와 파동의 이중성이라는 말이 참 그 자체로 이상한 게, 입자가 이미 파동의 성질을 보여주기 때문이다. 대표적인 게 큰 수의 법칙과 정규분포다. 과학자들이 말하는 파동의 성질이란게, 간섭효과에 의한 것인데 간섭효과 하면 큰 수의 법칙과 정규분포 아니겠는가. 동전을 계속 던져보면 바닥에 떨어진 동전의 면이 딱 떨어지지는 않지만 50:50의 확률에 수렴하는 걸 알 수 있는데, 이게 사실 신기한 거다. 동전을 100번 던졌다치고, 처음 던진 동전과 49번째, 100번째 던진 동전이 텔레파시를 하는 것도 아닌데, 어떻게 상대방이 뒤집힌 면을 기가막히게 알아서 자신은 반대로 뒤집어진단 말인가. 정규분포도 마찬가지다. 정규분포는 시행확률인데, 확률의 확률 정도로 이해하면 된다. 큰수의 법칙이 2단계로 일어난다는 말. 결혼한 부부가 아이를 낳을 때 옆집 부부한테 장래 아이의 키를 물어보는 것도 아닌데, 초등학교 교실에 가면 아이들 키의 분포가 정규분포를 이루고 있다. 이거 무슨 집단 텔레파시냐?
한편 이중슬릿실험의 해석도 웃긴게, 사람들은 간섭 무늬에만 신경쓸뿐, 간섭무늬 뒤에 고르게 퍼져있는 분포는 말하지 않는다는 거. 실험장치가 광자를 하나씩 발사해서 만든 누적분포인데, 광자들은 어떻게 앞서 발사된 놈의 위치를 알아서 자신은 다른 곳으로 날아가 박히네? 간섭무늬가 지 옆에 있는 광자의 영향을 받아서 생기는 거라는데, 벽에 골고루 박힌 입자들도 앞서 발사된 다른 놈한테 영향을 받은 거 아니냐? 왜 이런 건 말을 안 하느냐고. 군대에서 영점사격을 해보면 어느정도 연습을 하면 탄착점이 비교적 모이는 걸 알 수 있는데, 재밌는 건 그럼에도 불구하고 탄착점이 일정한 분포를 가지고 퍼진다는거. 물론 연습을 안 하면 분산의 크기가 커지긴 한다. 하지만 크기의 차이가 있을뿐 여전히 일정한 분포를 가진다는 본질은 변하지 않았다. 사실 이런 현상은 굳이 영점사격 아니더라도 그 어떤 정교한 발사기를 동원해도 반드시 일정한 분포와 오류(오차)를 동시에 가진다는 건, 사람들도 경험적으로 알지 않나. 그게 바로 정규분포다.

(이미지 안 올려짐. 첨부파일 확인 요망)
.jpg)
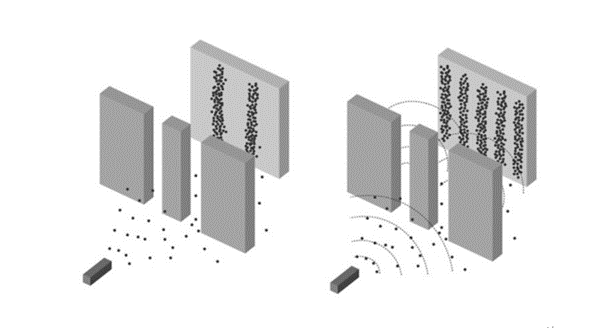
관찰자효과니 하는 게, 과학자들의 어설픈 설명으로 와전된 게 있지만, 본인이 유명 과학자들이 설명한 것을 보아도, 빛의 위치를 측정하려면 어떤 식으로든 영향을 줄 수밖에 없는 상황이더라.(이거 찾아보면 실험방법이 몇가지 되더만) 그들이 말하는 영향을 주지 않는 백만가지 객관적인 관찰을 조금만 들여다보면 죄다 영향을 주고 있더라는 말이다. 즉 관찰하면 입자요 안 하면 파동이라는 말은, 영향을 주면 입자요 없으면 파동이라는 말로 바뀌어야 한다. 이렇게 바꾸어놓고 생각하면 날아가는 놈한테 영향을 주면 당연히 영향을 받아 영향이 없을 때와는 다른 패턴이 생기게 마련이고, 그게 이중슬릿실험에서는 간섭무늬가 제거되는 걸로 나타난다. 그런데 말이다. 그럼에도 불구하고 여전히 광자들은 골고루 퍼져있더라는 거. 간섭무늬만 없어졌지 여전히 광자들은 서로한테 영향을 주고 있다. 이는 광자집단이 외부의 영향을 받아서, 혹은 제약을 받아서 패턴의 변화가 생겼지만 여전히 지들끼리 상호작용 하고 있는 걸로 이해할 수 있다.
정규분포나, 큰수의 법칙, 이중슬릿실험을 설명하려면 우리가 가정해야 할 것은 계의 존재다. 양자역학의 수많은 신기한 현상들은 계의 영향을 받지 않는 입자를 설정하기 때문에 생긴 해프닝이다. 계가 있다면 모든 게 깔끔해진다. 한 놈이 다른 놈에게 영향을 주려면 연결되어 있어야 하는데, 그게 바로 계다. 남친이 바뀌면 여친은 그즉시 변화를 포착하고 헤어질 결심을 하기 시작하는 데, 둘은 사회라는 계에 묶여있기 때문이다. 여자들이 말하는 육감이 마술 같은 게 아니라, 분위기 변화를 예민하게 파악하는 것이다. 남자들은 둔해서 분위기를 포착 못 하는 거고. 과학자들의 수행한 수많은 실험은 계의 존재(당시에는 에테르)를 부정하지만, 실험이 잘못된 것일 수도 있다. 그걸로는 계의 영향을 검출할 수 없다는 말이다. 하지만 과학자들이 암흑물질과 암흑에너지를 보지도 않고 예측하듯이, 파동의 성질을 매개하는 매질도 예측을 해야 하는 거 아닌가?
총을 쏜다면 앞서 발사된 총알을 사수가 기억하고 있다가 그걸 반영해서 오차를 수정하기 때문이 아니냐고 반문하겠지만, 총을 막대기로 묶어서 고정하고 쏘아도 총알은 절대로 한점에 계속 박히지 않는다. 니가 뭔 짓을 해도 분포와 오차가 생긴다는 말. 왜냐하면 총알이 날아가는 공기에 주기적인 변화가 숨어있기 때문이다. 보이지 않아도 뭔가가 있다. 승자의 저주라는 게 있는데, 요새 프리미어리그 득점왕 했던 손흥민과 살라가 삽질하는 거 보면 알 수 있는 현상이다. 겉으로 보기에 그들은 변한게 없지만, 뭔가 변한게 있다. 사람들이 그들을 관측하기 시작한 것이다. 유명세라는 게 원래 그런거. 외부의 영향이 포지션의 변화를 주었다. 요사이 손흥민은 패스 타이밍을 늘 놓치는데, 득점왕을 의식하기 때문이다. 득점왕이라면 스스로 골을 넣어야 한다고 생각하게 마련이다. 그 순간 패스 타이밍은 늦어지는 거고. 그런 손흥민이 토트넘의 팀플레이를 조지고 있다.
https://www.youtube.com/watch?v=XN3xBbRFkgQ 이중슬릿 실험 설명 영상
참고로 양자컴퓨팅은 필자가 좀 검색을 해봤는데, 한국이고 미국이고 그 어떤 과학자도 수식 이상의 설명을 하는 놈이 없더라. 그래서 양자역학의 얽힘과 중첩으로 대강 추측컨데, 부분과 전체가 한몸(간섭)이라는 성질을 이용해 병렬연산에 특화된 연산장치를 만들겠다는게 큐비트의 핵심 원리가 아닐까 한다. 기존 컴퓨터의 비트는 병렬연산을 할 때, 말이 병렬이지, 실제로는 하나씩 순서대로 분배하고 확인해야 하는 과정이 있지만, 큐비트는 전체가 부분과 서로 간섭하고 있으므로 이게 한방에 되므로 연산시간이 획기적으로 줄어든다는 말인듯. 컴공에서 말하는 log스케일(지수적)의 연산수 증가를 다항시간(선형증가)으로 줄인다는게 핵심. 문제는 이게 소인수분해같은 특수한 연산에만 특화되어 있다는 거. 소인수분해는 암호학과 관련이 있고, 이 이상 들어가려면 걔네들의 수식을 읽어야 하는데, 어느 세월에. 새끼들이 이해를 못 하니깐 죄다 수식만 쓰고 자빠졌네.












